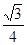题目内容
已知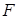 是抛物线
是抛物线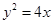 的焦点,准线与
的焦点,准线与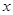 轴的交点为
轴的交点为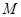 ,点
,点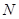 在抛物线上,且
在抛物线上,且 ,则
,则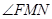 等于( )
等于( )
A.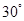 | B.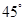 | C.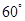 | D.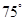 |
C
解析试题分析:
过N作NE垂直于准线与E,由抛物线的定义得|NE|=|NF|;在RT△ENM中求出∠EMN=30°.即可得到结论.解:过N作NE垂直于准线与E.
由抛物线的定义得:|NE|=|NF|.
在RT△ENM中因为|EN|=|NF|= |MN|.所以:∠EMN=30°.故:∠NMF=90°-∠EMN=60°.故选C
|MN|.所以:∠EMN=30°.故:∠NMF=90°-∠EMN=60°.故选C
考点:抛物线的简单性质
点评:本题主要考查抛物线的简单性质.解决问题的关键在于利用抛物线的定义得到|NE|=|NF|

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
设m是常数,若 是双曲线
是双曲线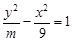 的一个焦点,则m的值为( )
的一个焦点,则m的值为( )
| A.16 | B.34 | C.16或34 | D.4 |
已知椭圆的焦点为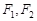 ,P是椭圆上一动点,如果延长F1P到Q,使
,P是椭圆上一动点,如果延长F1P到Q,使 ,那么动点Q的轨迹是( )
,那么动点Q的轨迹是( )
| A.椭圆 | B.双曲线 | C.抛物线 | D.圆 |
椭圆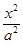 +
+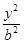 =1(a>b>0)上一点A关于原点的对称点为B, F为其右焦点, 若AF⊥BF, 设∠ABF=
=1(a>b>0)上一点A关于原点的对称点为B, F为其右焦点, 若AF⊥BF, 设∠ABF=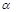 , 且
, 且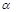 ∈[
∈[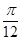 ,
,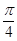 ], 则该椭圆离心率的取值范围为 ( )
], 则该椭圆离心率的取值范围为 ( )
A.[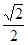 ,1 ) ,1 ) | B.[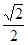 , ,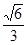 ] ] | C.[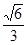 , 1) , 1) | D.[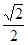 , ,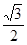 |
若焦点在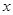 轴上的椭圆
轴上的椭圆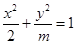 的离心率为
的离心率为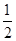 ,则
,则 的值为( )
的值为( )
A.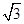 | B. | C. | D.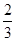 |
设抛物线的顶点在原点,准线方程为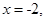 则抛物线的方程是( )
则抛物线的方程是( )
A.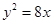 | B.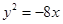 | C. | D. |
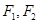 分别是双曲线
分别是双曲线 的左右焦点,
的左右焦点,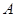 为双曲线的右顶点,线段
为双曲线的右顶点,线段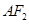 的垂直平分线交双曲线于
的垂直平分线交双曲线于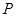 ,且
,且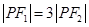 ,则双曲线的离心率为
,则双曲线的离心率为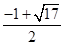
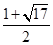
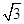
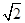
 的左焦点F(-c,0)(c >0),作圆:
的左焦点F(-c,0)(c >0),作圆: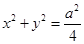 的切线,切点为E,延长FE交双曲线右支于点P,若
的切线,切点为E,延长FE交双曲线右支于点P,若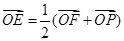 ,则双曲线的离心率为
,则双曲线的离心率为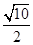



 等边三角形的圆锥,过底面圆周上任一点作一平面
等边三角形的圆锥,过底面圆周上任一点作一平面 ,且
,且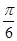 ,已知
,已知