题目内容
5．已知直线l：x+2y=0，圆C：x2+y2-6x-2y-15=0，直线l被圆所截得的线段长为$4\sqrt{5}$．分析 根据圆的方程找出圆心坐标和半径，过点A作AC⊥弦BD，可得C为BD的中点，根据勾股定理求出BC，即可求出弦长BD的长．
解答 
解：过点A作AC⊥弦BD，垂足为C，连接AB，可得C为BD的中点．
由x2+y2-6x-2y-15=0，得（x-3）2+（y-1）2=25．
知圆心A为（3，1），r=5．
由点A（3，1）到直线x+2y=0的距离AC=$\frac{|3+2|}{\sqrt{5}}$=$\sqrt{5}$．
在直角三角形ABC中，AB=5，AC=$\sqrt{5}$，
根据勾股定理可得BC=$\sqrt{25-5}$=2$\sqrt{5}$，
则弦长BD=2BC=$4\sqrt{5}$．
故答案为：$4\sqrt{5}$．
点评 本题考查学生灵活运用垂径定理解决实际问题的能力，灵活运用点到直线的距离公式及勾股定理化简求值，会利用数形结合的数学思想解决数学问题，是一道综合题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．已知函数f（x）=a-x2（1≤x≤2）与g（x）=x+1的图象上存在关于x轴对称的点，则实数a的取值范围是（ ）
| A． | $[-\frac{5}{4}，+∞）$ | B． | [1，2] | C． | $[-\frac{5}{4}，1]$ | D． | [-1，1] |
16．下列各组函数中，表示同一函数的是（ ）
| A． | $y=x+1与y=\frac{{{x^2}+x}}{x}$ | B． | $f（x）=\frac{x^2}{{{{（{\sqrt{x}}）}^2}}}与g（x）=x$ | ||
| C． | $f（x）=x\frac{|x|}{x}与f（t）=\left\{\begin{array}{l}t（t＞0）\\-t（t＜0）\end{array}\right.$ | D． | $f（x）=|x|与g（x）=\left\{\begin{array}{l}x（x＞0）\\-x（x＜0）\end{array}\right.$ |
20．将函数f（x）=sin2x的图象向左平移$\frac{π}{4}$个长度单位，得到函数g（x）的图象，则g（x）的单调递增区间是（ ）
| A． | （kπ-$\frac{π}{2}$，kπ）（k∈Z） | B． | （kπ，kπ+$\frac{π}{2}$）（k∈Z） | C． | （kπ-$\frac{π}{4}$，kπ+$\frac{π}{4}$）（k∈Z） | D． | （kπ+$\frac{π}{4}$，kπ+$\frac{3π}{4}$）（k∈Z） |
17．
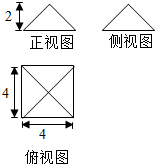图为某个几何体的三视图，则该几何体的表面积为（ ）
图为某个几何体的三视图，则该几何体的表面积为（ ）| A． | 32 | B． | 16+16$\sqrt{2}$ | C． | 48 | D． | 16+32$\sqrt{2}$ |