题目内容
15.已知数列{an}的前n项和Sn ,点(n,$\frac{{S}_{n}}{n}$)在直线y=2x+1上,数列{bn}满足$\frac{{b}_{1}-1}{3}$+$\frac{{b}_{2}-1}{{3}^{2}}$+…+$\frac{{b}_{n}-1}{{3}^{n}}$=an(n∈N*).(1)求数列{an}的通项公式;
(2)求数列{bn}的前n项和Tn;
(3)是否存在常数p(p≠-1),使数列{$\frac{{T}_{n}-n}{3({3}^{n}+p)}$}是等比数列?若存在,求出p的值;若不存在,请说明理由.
分析 (1)通过将点(n,$\frac{{S}_{n}}{n}$)代入直线y=2x+1方程,当n≥2时利用an=Sn-Sn-1计算即得结论;
(2)由(1)及当n≥2时利用$\frac{{b}_{1}-1}{3}$+$\frac{{b}_{2}-1}{{3}^{2}}$+…+$\frac{{b}_{n}-1}{{3}^{n}}$=an与$\frac{{b}_{1}-1}{3}$+$\frac{{b}_{2}-1}{{3}^{2}}$+…+$\frac{{b}_{n-1}-1}{{3}^{n-1}}$=an-1作差,计算可得数列{bn}的通项公式,进而计算可得结论;
(3)通过(2)可知$\frac{{T}_{1}-1}{3(3+p)}$=$\frac{3}{3+p}$,当n≥2时$\frac{{T}_{n}-n}{3({3}^{n}+p)}$=2•$\frac{{3}^{n}-\frac{3}{2}}{{3}^{n}+p}$,通过令p=-$\frac{3}{2}$比较即得结论.
解答 解:(1)∵点(n,$\frac{{S}_{n}}{n}$)在直线y=2x+1上,
∴$\frac{{S}_{n}}{n}$=2n+1,即Sn=2n2+n,
当n≥2时,an=Sn-Sn-1=4n-1,
又∵a1=2+1=3满足上式,
∴数列{an}的通项公式an=4n-1;
(2)∵数列{bn}满足$\frac{{b}_{1}-1}{3}$+$\frac{{b}_{2}-1}{{3}^{2}}$+…+$\frac{{b}_{n}-1}{{3}^{n}}$=an(n∈N*),
∴当n≥2时,$\frac{{b}_{n}-1}{{3}^{n}}$=an-an-1=4,
∴bn=1+4•3n,
又∵$\frac{{b}_{1}-1}{3}$=3即b1=10不满足上式,
∴bn=$\left\{\begin{array}{l}{10,}&{n=1}\\{1+4•{3}^{n},}&{n≥2}\end{array}\right.$,
∴Tn=$\left\{\begin{array}{l}{10,}&{n=1}\\{-9+n+2•{3}^{n+1},}&{n≥2}\end{array}\right.$;
(3)结论:存在常数p=-$\frac{3}{2}$,使数列{$\frac{{T}_{n}-n}{3({3}^{n}+p)}$}是等比数列.
理由如下:
由(2)可知$\frac{{T}_{1}-1}{3(3+p)}$=$\frac{3}{3+p}$,
当n≥2时,$\frac{{T}_{n}-n}{3({3}^{n}+p)}$=2•$\frac{{3}^{n}-\frac{3}{2}}{{3}^{n}+p}$,
令p=-$\frac{3}{2}$,则$\frac{{T}_{n}-n}{3({3}^{n}+p)}$=2(n≥2),此时$\frac{{T}_{1}-1}{3(3+p)}$=2,
∴数列{$\frac{{T}_{n}-n}{3({3}^{n}+p)}$}是常数项,即为公比为1的等比数列.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 平行 | B. | 相交 | C. | 在平面内 | D. | 都有可能 |
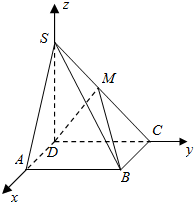 如图,在四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,点M在侧棱SC上,∠ABM=60°.若以DA,DC,DS,分别为x轴,y轴,z轴建立如图所示的空间直角坐标系D-xyz,则M的坐标为(0,1,1).
如图,在四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,点M在侧棱SC上,∠ABM=60°.若以DA,DC,DS,分别为x轴,y轴,z轴建立如图所示的空间直角坐标系D-xyz,则M的坐标为(0,1,1).