题目内容
已知递增等差数列 前3项的和为
前3项的和为 ,前3项的积为8,
,前3项的积为8,
(1)求等差数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 。
。
(1)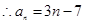 (2)
(2)
解析试题分析:本题第(1)问,要得到等差数列的通项公式,需要首项和公差,而由前3项的和为 ,前3项的积为8可得
,前3项的积为8可得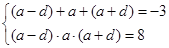 ,这个可解出首项和公差,需要注意的是,由于数列递增数列,则
,这个可解出首项和公差,需要注意的是,由于数列递增数列,则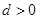 ;第(2)问,在(1)中,已经得到数列
;第(2)问,在(1)中,已经得到数列 的通项公式
的通项公式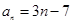 ,把它代入
,把它代入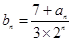 得:
得: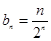 ,进而用错位相减法得到
,进而用错位相减法得到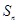 ,这种方法常用于求一般数列的通项公式和前n项和。
,这种方法常用于求一般数列的通项公式和前n项和。
解:(1)等差数列的前三项为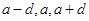 ,则
,则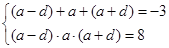
解得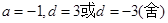
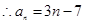
(2)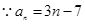
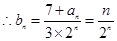
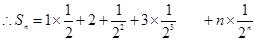 (1)
(1)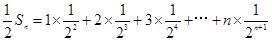 (2)
(2)
(1)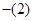
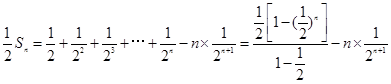

考点:等差数列的前n项和.
点评:本题主要考查了等差数列性质及通项公式、求和公式的应用,属于基础性试题。

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
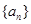 为递增等差数列,且
为递增等差数列,且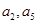 是方程
是方程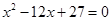 的两根.数列
的两根.数列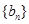 为等比数列,且
为等比数列,且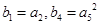 .
.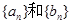 的通项公式;
的通项公式;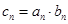 ,求数列
,求数列 的前
的前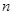 项和
项和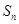 .
.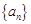 的前n项和为Sn,且
的前n项和为Sn,且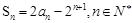 .
. ,记数列
,记数列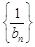 的前
的前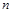 项和为
项和为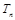 .求证:
.求证: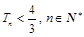 .
. 的公差
的公差 ,它的前
,它的前 项和为
项和为 ,若
,若 ,且
,且 成等比数列.(1) 求数列
成等比数列.(1) 求数列 的前
的前 ,求证:
,求证: .
. 中,已知
中,已知 (
(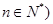 .
. 及
及 ;
; 的前
的前 项和
项和 .
. 满足:
满足: ,
, 项和为
项和为 。
。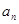 及
及 (其中
(其中 为常数,且
为常数,且 ),求证数列
),求证数列 为等比数列。
为等比数列。 的前
的前 项和
项和 (
( ,求证:数列
,求证:数列 是等差数列,并求数列
是等差数列,并求数列 ,
, ,求使得
,求使得 成立的最小正整数
成立的最小正整数 中,
中, ,公差
,公差 为整数,若
为整数,若 ,
, .
. 项和
项和 的最大值;
的最大值;  的前三项和为18,
的前三项和为18, 是一个与
是一个与 无关的常数,若
无关的常数,若 恰为等比数列
恰为等比数列 的前三项,(1)求
的前三项,(1)求 ,
, 的前三
的前三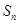 ,求证:
,求证: