题目内容
设数列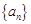 的前n项和为Sn,且
的前n项和为Sn,且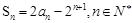 .
.
(1)求数列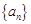 的通项公式;
的通项公式;
(2)令 ,记数列
,记数列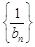 的前
的前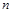 项和为
项和为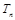 .求证:
.求证: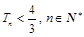 .
.
(1)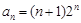 ;(2)详见试题解析.
;(2)详见试题解析.
解析试题分析:(1)先令 求得
求得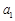 ,再利用
,再利用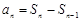 得
得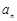 的递推式
的递推式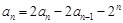 ,构造等差数列
,构造等差数列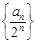 求得数列
求得数列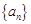 的通项公式;(2)在(1)的基础上,先求
的通项公式;(2)在(1)的基础上,先求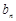 ,根据
,根据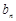 的结构特征利用放缩法证明
的结构特征利用放缩法证明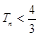 .
.
试题解析:(1)由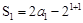 得
得 .由
.由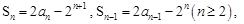 两式相减得
两式相减得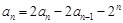 ,即
,即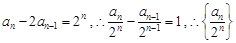 是以为
是以为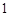 公差的等差数列.
公差的等差数列.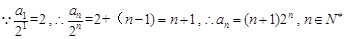 . 6分
. 6分
(2)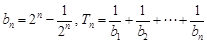 .
.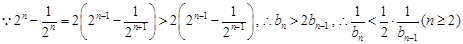 .当
.当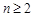 时,
时,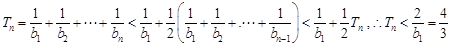 .
.
当 时,
时,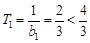 .
.
综上,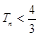 . 13分
. 13分
考点:1、数列通项公式的求法;2、数列不等式的证明.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
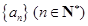 的前
的前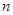 项和为
项和为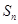 ,且
,且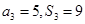 .
.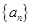 的通项公式;
的通项公式;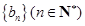 ,若
,若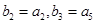 ,求数列
,求数列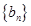 的前
的前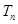
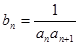 ,求数列
,求数列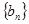 的前
的前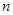 项和
项和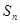
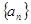 满足
满足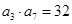 ,
,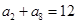 ,且
,且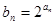 (
(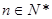 ).
). ,求数列
,求数列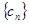 的前n项和
的前n项和 .
.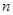 项的和
项的和 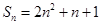 ,求数列的通项公式.
,求数列的通项公式. 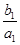 +
+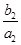 +…+
+…+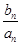 =1-
=1-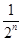 ,n∈N*,求{bn}的前n项和Tn.
,n∈N*,求{bn}的前n项和Tn. 的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n
的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n ·bn+1(
·bn+1( +
+ +
+ + +
+ + 与
与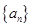 中,点
中,点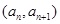
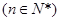 在直线
在直线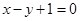 上,且
上,且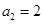 .
. 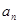 ;
;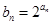 ,数列
,数列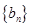 的前
的前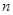 项和为
项和为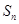 ,
,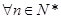 ,
,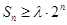 成立,求实数
成立,求实数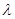 的取值范围.
的取值范围. 前3项的和为
前3项的和为 ,前3项的积为8,
,前3项的积为8, ,求数列
,求数列 的前
的前 项和
项和 。
。 中,当
中,当 时,总有
时,总有 成立,且
成立,且 .
. 是等差数列,并求数列
是等差数列,并求数列 项和
项和 .
.