题目内容
已知数列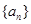 为递增等差数列,且
为递增等差数列,且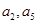 是方程
是方程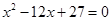 的两根.数列
的两根.数列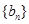 为等比数列,且
为等比数列,且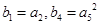 .
.
(Ⅰ)求数列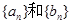 的通项公式;
的通项公式;
(Ⅱ)若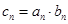 ,求数列
,求数列 的前
的前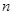 项和
项和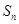 .
.
(Ⅰ)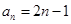 ,
,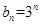 ;(Ⅱ)
;(Ⅱ)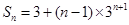 .
.
解析试题分析:(Ⅰ)解方程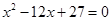 可得:
可得: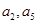 ,代入等差数列的通项公式可得其公差和首项,从而得数列
,代入等差数列的通项公式可得其公差和首项,从而得数列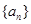 的通项公式;再由
的通项公式;再由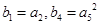 求得
求得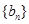 的公比和首项,从而求得
的公比和首项,从而求得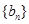 的通项公式.
的通项公式.
(Ⅱ)凡是由等差数列与等比数列的积构成的数列,求其和都用错位相减法.本题中求数列 的前
的前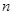 项和
项和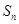 就用错位相消法.
就用错位相消法.
试题解析:(Ⅰ)解方程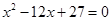 得:
得: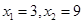 .
.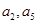 是方程
是方程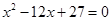 的两根,且数列
的两根,且数列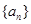 为递增等差数列,
为递增等差数列,
所以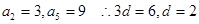
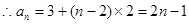 .
.
又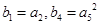 ,得
,得 ,所以
,所以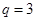 ,
,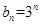 .
.
(Ⅱ) ,所以
,所以 ………………………………①
………………………………①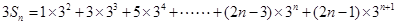 ……………………………②
……………………………②
①-②得: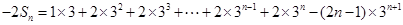
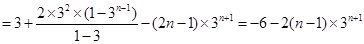
所以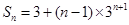 .
.
考点:1、等差数列等比数列的通项公式;2、错位相消法求和.

练习册系列答案
相关题目
 时,其前n项和满足
时,其前n项和满足 .
. ,数列{bn}的前n项和为
,数列{bn}的前n项和为 ,求
,求 的前
的前 项和为
项和为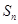 ,且
,且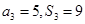 .
.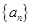 的通项公式;
的通项公式;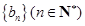 ,若
,若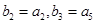 ,求数列
,求数列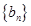 的前
的前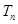
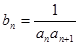 ,求数列
,求数列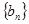 的前
的前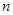 项和
项和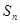
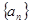 是等差数列,且
是等差数列,且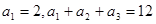
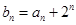 ,求数列
,求数列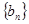 前n项和
前n项和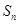 .
.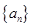 满足
满足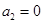 ,
,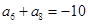 .
.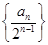 的前n项和.
的前n项和. 满足:
满足: ,
, .
. 及
及 ,求数列
,求数列 的前n项和
的前n项和 .
.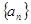 满足
满足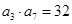 ,
,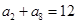 ,且
,且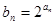 (
(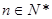 ).
). ,求数列
,求数列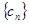 的前n项和
的前n项和 .
.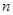 项的和
项的和 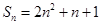 ,求数列的通项公式.
,求数列的通项公式.  前3项的和为
前3项的和为 ,前3项的积为8,
,前3项的积为8, ,求数列
,求数列 的前
的前 项和
项和 。
。