题目内容
2.已知圆心为C的圆:x2+y2+2x-4y+m=0与直线2x+y-3=0相交于A、B两点(1)若△ABC为正三角形,求m的值;
(2)是否存在常数m,使以AB为直径的圆经过坐标原点?若存在,求出m的值;若不存在,请说明理由.
分析 (1)求得圆的圆心和半径,由正三角形的性质,可得C到AB的距离d=$\frac{\sqrt{3}}{2}$r,计算可得m的值;
(2)假设存在常数m,使以AB为直径的圆经过坐标原点.即有OA⊥OB,取AB的中点M,连接OM,CM,即有OM=$\frac{1}{2}$AB=$\sqrt{{r}^{2}-{d}^{2}}$,由直线垂直的条件,由直线的交点可得M的坐标,运用两点的距离公式,解方程可得m,进而判断存在.
解答 解:(1)圆:x2+y2+2x-4y+m=0的圆心C(-1,2),
半径为r=$\sqrt{5-m}$,
由△ABC为正三角形,可得C到AB的距离d=$\frac{\sqrt{3}}{2}$r,
即为$\frac{|-2+2-3|}{\sqrt{5}}$=$\frac{\sqrt{3}}{2}$•$\sqrt{5-m}$,
解得m=$\frac{13}{5}$;
(2)假设存在常数m,使以AB为直径的圆经过坐标原点.
即有OA⊥OB,取AB的中点M,连接OM,CM,
即有OM=$\frac{1}{2}$AB=$\sqrt{{r}^{2}-{d}^{2}}$,
由CM⊥AB,可得CM的方程为y-2=$\frac{1}{2}$(x+1),
联立直线2x+y-3=0,可得M($\frac{1}{5}$,$\frac{13}{5}$),
即有$\sqrt{\frac{1}{25}+\frac{169}{25}}$=$\sqrt{5-m-\frac{9}{5}}$,
解得m=-$\frac{18}{5}$.
则存在常数m=-$\frac{18}{5}$,使以AB为直径的圆经过坐标原点.
点评 本题考查直线和圆的位置关系,考查弦长公式和正三角形的性质,以及直角三角形的性质,属于中档题.

| A. | {-1,2} | B. | {1,2} | C. | {0,1,2} | D. | {2} |
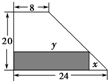 某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,当截取的矩形面积最大时,矩形两边长x、y应为15,12.
某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,当截取的矩形面积最大时,矩形两边长x、y应为15,12. 如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,M为AD上一点且AM=2DM.
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,M为AD上一点且AM=2DM.