题目内容
17．若（1-ax）6的展开式中的x3项的系数为20，则实数a=-1．分析 在二项展开式的通项公式中，令x的幂指数等于3，求出r的值，即可求得x3项的系数，再根据x3项的系数等于60，求得实数a的值．
解答 解：（1-ax）6的展开式的通项公式为Tr+1=${C}_{6}^{r}$•（-a）r•xr，令r=3，
可得展开式中的x3项的系数为（-a）3 ${C}_{6}^{3}$=-20a3=20，
故a=-1，
故答案为：-1．
点评 本题主要考查二项式定理的应用，二项展开式的通项公式，属于基础题．
练习册系列答案
相关题目
7．用反证法证明命题：“三个连续正整数a，b，c中至少有一个能被2整除”时，要做的假设是（ ）
| A． | 假设三个连续正整数a，b，c都不能被2整除 | |
| B． | 假设三个连续正整数a，b，c都能被2整除 | |
| C． | 假设三个连续正整数a，b，c至多有一个能被2整除 | |
| D． | 假设三个连续正整数a，b，c至多有两个能被2整除 |
8．若直线y=kx+1与圆x2+y2=1相交与P，Q两点，且此圆被分成的两段弧长之比为1：2，则k的值为（ ）
| A． | $-\sqrt{3}$或$\sqrt{3}$ | B． | $\sqrt{3}$ | C． | $-\sqrt{2}$或$\sqrt{2}$ | D． | $\sqrt{2}$ |
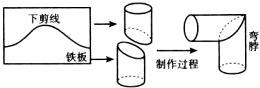铁匠师傅在打制烟筒弯脖时，为确保对接成直角，在铁板上的下剪线正好是余弦曲线$y=acos\frac{x}{a}$的一个周期的图象如图，当弯脖的直径为12cm时，a应是6cm．
20．“x＞3”是“x＞2”的（ ）
| A． | 必要不充分条件 | B． | 充分不必要条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |