题目内容
20．（1-$\frac{2}{x}$）4展开式中$\frac{1}{x}$的系数是-8．分析 先求出二项式展开式的通项公式，再令x的幂指数等于-1，求得r的值，即可求得展开式中$\frac{1}{x}$的系数．
解答 解：（1-$\frac{2}{x}$）4展开式的通项公式为Tr+1=${C}_{4}^{r}$•（-2）r•x-r，令-r=-1，可得r=1，
故展开式中$\frac{1}{x}$的系数是${C}_{4}^{1}$•（-2）=-8，
故答案为：-8．
点评 本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，属于基础题．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
11．在平面直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴建立极坐标系，点M的直角坐标是（1，-$\sqrt{3}$），则点M的极坐标为（ ）
| A． | （2，-$\frac{π}{3}$） | B． | （2，$\frac{π}{3}$） | C． | （2，$\frac{2π}{3}$） | D． | （2，2kπ+$\frac{π}{3}$）（k∈Z） |
8．若直线y=kx+1与圆x2+y2=1相交与P，Q两点，且此圆被分成的两段弧长之比为1：2，则k的值为（ ）
| A． | $-\sqrt{3}$或$\sqrt{3}$ | B． | $\sqrt{3}$ | C． | $-\sqrt{2}$或$\sqrt{2}$ | D． | $\sqrt{2}$ |
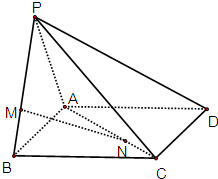如图，在四棱锥P-ABCD中，侧面PAB⊥底面ABCD，侧面PAB是边长为3的等边三角形，底面ABCD是正方形，M是侧棱PB上的点，N是底面对角线AC上的点，且PM=2MB，AN=2NC．