题目内容
【题目】已知函数f（x）=sin（x+
）+sin（x﹣）+cosx．
（Ⅰ）求f（x）的最小正周期；
（Ⅱ）在△ABC中，f（A）=
，△ABC的面积为，AB=
，求BC的长．
【答案】（Ⅰ）
（Ⅱ）2或
【解析】
（1）先根据两角和与差正弦公式展开，再根据配角公式得基本三角函数形式，最后根据正弦函数周期公式求结果，（2）先求A,再根据面积公式求不，最后根据余弦定理求a.
函数f（x）=sin（x+
）+sin（x﹣）+cosx．
化简可得：f（x）=2sinxcos+cosx=
sinx+cosx=2sin（x+）
（Ⅰ）f（x）的最小正周期T=
；
（Ⅱ）由f（A）=
，即2sin（A+）=，
∴sin（A+）=
，
∵0＜A＜π，
∴＜（A+）
．
可得：（A+）=
或
则A=或A=
．
当则A=时，△ABC的面积为
=
bcsinA，AB=c=
，
∴b=AC=2
余弦定理：BC2=22+（2
）2﹣2×
×cos，
解得：BC=2
当A=时，△ABC的面积为=bc，AB=c=，
∴b=AC=1
直角三角形性质可得：BC2=22+（2）2，
解得：BC=
．
故答案为：2或
【题目】某种产品的质量以其质量指标值来衡量，质量指标值越大表明质量越好，记其质量指标值为
，当
时，产品为一级品；当
时，产品为二级品，当
时，产品为三级品，现用两种新配方（分别称为
配方和
配方）做实验，各生产了
件这种产品，并测量了每件产品的质量指标值，得到下面的试验结果 ：（以下均视频率为概率）
配方的频数分配表：
指标值分组 |
|
|
|
|
频数 |
|
|
|
|
配方的频数分配表：
指标值分组 |
|
|
|
|
|
频数 |
|
|
|
|
|
（1）若从配方产品中有放回地随机抽取
件，记“抽出的配方产品中至少
件二级品”为事件
，求事件发生的概率
；
（2）若两种新产品的利润率
与质量指标满足如下关系：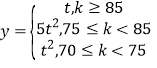
，其中
，从长期来看，投资哪种配方的产品平均利润率较大？
