题目内容
【题目】已知函数
.
（1）讨论函数
的单调性；
（2）若
，函数在区间
上恰有两个零点，求
的取值范围.
【答案】（1）详见解析；（2）
.
【解析】
（1）求出
，对
的正负分类讨论即可。
（2）利用（1）中的结论即可判断
在
上单调递减，在
上单调递增，对
与区间
的关系分类讨论即可判断在的单调性，从而根据零点个数列不等式组即可求解。
解：（1）
的定义域为
，
.
①
时，
，所以在上单调递增；
②
时，由得
，
得
.
即在上单调递减，在上单调递增.
综上：当时，在上单调递减；
当时，在上单调递减，在上单调递增.
（2）当时，由（1）知在上单调递减，在上单调递增，
①若
，即
时，在上单调递增，
，在区间上无零点.
②若
，即
时，在
上单调递减，在
上单调递增，
.
∵在区间上恰有两个零点，
∴
，∴
.
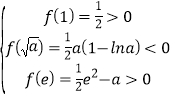③若
，即
时，在上单调递减，
，
，在区间上有一个零点.
综上，在区间上恰有两个零点时的取值范围是
.
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
相关题目
【题目】某脐橙种植基地记录了10棵脐橙树在未使用新技术的年产量（单位：
）和使用了新技术后的年产量的数据变化，得到表格如下：
未使用新技术的10棵脐橙树的年产量
第一棵 | 第二棵 | 第三棵 | 第四棵 | 第五棵 | 第六棵 | 第七棵 | 第八棵 | 第九棵 | 第十棵 | |
年产量 | 30 | 32 | 30 | 40 | 40 | 35 | 36 | 45 | 42 | 30 |
使用了新技术后的10棵脐橙树的年产量
第一棵 | 第二棵 | 第三棵 | 第四棵 | 第五棵 | 第六棵 | 第七棵 | 第八棵 | 第九棵 | 第十棵 | |
年产量 | 40 | 40 | 35 | 50 | 55 | 45 | 42 | 50 | 51 | 42 |
已知该基地共有20亩地，每亩地有50棵脐橙树.
（1）估计该基地使用了新技术后，平均1棵脐橙树的产量；
（2）估计该基地使用了新技术后，脐橙年总产量比未使用新技术将增产多少？
（3）由于受市场影响，导致使用新技术后脐橙的售价由原来（未使用新技术时）的每千克10元降为每千克9元，试估计该基地使用新技术后脐橙年总收入比原来增加的百分数.
