题目内容
【题目】给定平面上的五个点A、B、C、D、E,任意三点不共线.由这些点连成4条线,每点至少是一条线段的端点,不同的联结方式有 种.
【答案】135
【解析】
图中,4种联结方式都满足题目要求 (图中仅表示点.线间联结形式不考虑点位置).
 (1)
(1)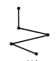 (2)
(2)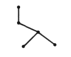 (3)
(3)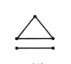 (4)
(4)
情形(1),情形根据中心点的选择,有5种联结方式;
情形(2),可视为5个点A、B、C、D、E的排列,但一种排列与其逆序排列是同一的,且两者是——对应的,则联结方式有![]() 种;
种;
情形(3),首先是分歧点的选择有5种,其次是分叉的两点的选择有![]() 种,最后是余下并连两点的顺序有别,有2!种.共有5×6×2=60种;
种,最后是余下并连两点的顺序有别,有2!种.共有5×6×2=60种;
情形(4),选择三点构造三角形,有![]() 种.
种.
总计5+60+60+10=135种联结方式.

 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案【题目】“一本书,一碗面,一条河,一座桥”曾是兰州的城市名片,而现在“兰州马拉松”又成为了兰州的另一张名片,随着全民运动健康意识的提高,马拉松运动不仅在兰州,而且在全国各大城市逐渐兴起,参与马拉松训练与比赛的人口逐年增加.为此,某市对人们参加马拉松运动的情况进行了统计调查.其中一项调查是调查人员从参与马拉松运动的人中随机抽取200人,对其每周参与马拉松长跑训练的天数进行统计,得到以下统计表:
平均每周进行长跑训练天数 | 不大于2天 | 3天或4天 | 不少于5天 |
人数 | 30 | 130 | 40 |
若某人平均每周进行长跑训练天数不少于5天,则称其为“热烈参与者”,否则称为“非热烈参与者”.
(1)经调查,该市约有2万人参与马拉松运动,试估计其中“热烈参与者”的人数;
(2)根据上表的数据,填写下列2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“热烈参与马拉松”与性别有关?
热烈参与者 | 非热烈参与者 | 合计 | |
男 | 140 | ||
女 | 55 | ||
合计 |
附:k2=![]() (n为样本容量)
(n为样本容量)
P(k2≥k0) | 0.500 | 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】为了解某地区观众对大型综艺活动《中国好声音》的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众收看该节目的场数与所对应的人数表:
场数 | 9 | 10 | 11 | 12 | 13 | 14 |
人数 | 10 | 18 | 22 | 25 | 20 | 5 |
将收看该节目场次不低于13场的观众称为“歌迷”,已知“歌迷”中有10名女性.
(1)根据已知条件完成下面的2×2列联表,并据此资料我们能否有95%的把握认为“歌迷”与性别有关?
非歌迷 | 歌迷 | 合计 | |
男 | |||
女 | |||
合计 |
(2)将收看该节目所有场次(14场)的观众称为“超级歌迷”,已知“超级歌迷”中有2名女性,若从“超级歌迷”中任意选取2人,求至少有1名女性观众的概率.
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
附:K2=![]() .
.