题目内容
【题目】设![]() :实数
:实数![]() 满足不等式
满足不等式![]() ,
,![]() :函数
:函数![]() 无极值点.
无极值点.
(1)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若“![]() 为真命题”是“
为真命题”是“![]() ”的必要不充分条件,求正整数
”的必要不充分条件,求正整数![]() 的值.
的值.
【答案】(1)![]() 或
或![]() .(2)
.(2)![]()
【解析】
(1)分别求得![]() 为真和
为真和![]() 为真时
为真时![]() 的范围,由“
的范围,由“![]() ”为假命题,“
”为假命题,“![]() ”为真命题可得
”为真命题可得![]() 与
与![]() 只有一个命题是真命题,进而分类讨论求解即可;
只有一个命题是真命题,进而分类讨论求解即可;
(2)由“![]() ”为真命题可得
”为真命题可得![]() ,解得不等式
,解得不等式![]() 为
为![]() ,由必要不充分条件可得
,由必要不充分条件可得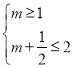 (两个不等式不能同时取等号),进而求解.
(两个不等式不能同时取等号),进而求解.
(1)若![]() 为真,则
为真,则![]() ,解得
,解得![]() ;
;
若![]() 为真,则函数
为真,则函数![]() 无极值点,所以
无极值点,所以![]() 恒成立,
恒成立,
则![]() ,解得
,解得![]() ,
,
因为“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,
”为真命题,
所以![]() 与
与![]() 只有一个命题是真命题,
只有一个命题是真命题,
若![]() 为真命题,
为真命题,![]() 为假命题,则
为假命题,则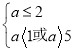 ,解得
,解得![]() ;
;
若![]() 为真命题,
为真命题,![]() 为假命题,则
为假命题,则![]() ,解得
,解得![]() .
.
综上,实数![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.
(2)因为“![]() ”为真命题,所以
”为真命题,所以![]()
![]() 都为真命题,
都为真命题,
所以![]() ,解得
,解得![]() ;
;
因为![]() ,所以
,所以![]() ,
,
因为必要不充分条件,所以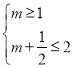 (两个不等式不能同时取等号),
(两个不等式不能同时取等号),
解得![]() ,
,
又因为![]() ,所以
,所以![]() .
.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案【题目】某脐橙种植基地记录了10棵脐橙树在未使用新技术的年产量(单位:![]() )和使用了新技术后的年产量的数据变化,得到表格如下:
)和使用了新技术后的年产量的数据变化,得到表格如下:
未使用新技术的10棵脐橙树的年产量
第一棵 | 第二棵 | 第三棵 | 第四棵 | 第五棵 | 第六棵 | 第七棵 | 第八棵 | 第九棵 | 第十棵 | |
年产量 | 30 | 32 | 30 | 40 | 40 | 35 | 36 | 45 | 42 | 30 |
使用了新技术后的10棵脐橙树的年产量
第一棵 | 第二棵 | 第三棵 | 第四棵 | 第五棵 | 第六棵 | 第七棵 | 第八棵 | 第九棵 | 第十棵 | |
年产量 | 40 | 40 | 35 | 50 | 55 | 45 | 42 | 50 | 51 | 42 |
已知该基地共有20亩地,每亩地有50棵脐橙树.
(1)估计该基地使用了新技术后,平均1棵脐橙树的产量;
(2)估计该基地使用了新技术后,脐橙年总产量比未使用新技术将增产多少?
(3)由于受市场影响,导致使用新技术后脐橙的售价由原来(未使用新技术时)的每千克10元降为每千克9元,试估计该基地使用新技术后脐橙年总收入比原来增加的百分数.
【题目】为了解某地区观众对大型综艺活动《中国好声音》的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众收看该节目的场数与所对应的人数表:
场数 | 9 | 10 | 11 | 12 | 13 | 14 |
人数 | 10 | 18 | 22 | 25 | 20 | 5 |
将收看该节目场次不低于13场的观众称为“歌迷”,已知“歌迷”中有10名女性.
(1)根据已知条件完成下面的2×2列联表,并据此资料我们能否有95%的把握认为“歌迷”与性别有关?
非歌迷 | 歌迷 | 合计 | |
男 | |||
女 | |||
合计 |
(2)将收看该节目所有场次(14场)的观众称为“超级歌迷”,已知“超级歌迷”中有2名女性,若从“超级歌迷”中任意选取2人,求至少有1名女性观众的概率.
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
附:K2=![]() .
.