Question

【题目】已知函数f（x）=x2+ax﹣lnx，a∈R．
（1）若函数f（x）在[1，2]上是减函数，求实数a的取值范围；
（2）令g（x）=f（x）﹣x2 ， 是否存在实数a，当x∈（0，e]（e是自然常数）时，函数g（x）的最小值是3，若存在，求出a的值；若不存在，说明理由．

Answer 1

【答案】
（1）解： 在[1，2]上恒成立，

令h（x）=2x2+ax﹣1，

有

得 ，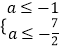

得

（2）解：假设存在实数a，使g（x）=ax﹣lnx（x∈（0，e]）有最小值3， =

当a≤0时，g（x）在（0，e]上单调递减，g（x）min=g（e）=ae﹣1=3， （舍去），

∴g（x）无最小值．

当 时，g（x）在 上单调递减，在 上单调递增

∴ ，a=e2，满足条件．

当 时，g（x）在（0，e]上单调递减，g（x）min=g（e）=ae﹣1=3， （舍去），

∴f（x）无最小值．

综上，存在实数a=e2，使得当x∈（0，e]时g（x）有最小值3．

【解析】（1）由函数f（x）在[1，2]上是减函数得 在[1，2]上恒成立，即有h（x）=2x2+ax﹣1≤0成立求解．（2）先假设存在实数a，求导得 = ，a在系数位置对它进行讨论，结合x∈（0，e]分当a≤0时，当 时，当 时三种情况进行．