Question

【题目】某个体经营者把开始六个月试销A、B两种商品的逐月投资与所获纯利润列成下表：

投资A商品金额（万元）	1	2	3	4	5	6
获纯利润（万元）	0.65	1.39	1.85	2	1.84	1.40
投资B商品金额（万元）	1	2	3	4	5	6
获纯利润（万元）	0.25	0.49	0.76	1	1.26	1.51

该经营者准备下月投入12万元经营这两种产品，但不知投入A、B两种商品各多少才最合算．请你帮助制定一下资金投入方案，使得该经营者能获得最大利润，并按你的方案求出该经营者下月可获得的最大利润（结果保留两个有效数字）．

Answer 1

【答案】分别投资A、B两种商品3.2万元和8.8万元，可获最大利润4.1万元

【解析】

根据表格数据，画出散点图，从而求出函数模型，再设第7个月投入A，B两种商品的资金分别为x万元，总利润为万元，求出利润函数，利用配方法，即可得到结论．

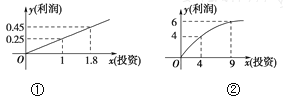
以投资额为横坐标，纯利润为纵坐标，在直角坐标系中画出散点图（如下图）．

据此，可考虑用下列函数分别描述上述两组数据之间的对应关系：

① ②

把，代入①式，得，解得

故前六个月所获纯利润关于月投资于A种商品的金额的函数关系式可近似的用

表示

再把，代入②式，得，故前六个月所获纯利润关于月投资于

B种商品的金额的函数关系式可近似的用表示

设下月投资于A种商品x万元，则投资于B种商品万元，可获纯利润：

当时，

故下月分别投资A、B两种商品3.2万元和8.8万元，可获最大利润4.1万元