题目内容
设点P(x,y)是圆(x-3)2+(y-4)2=1上任一点,若不等式x-y+c≤0恒成立,则c的取值范围是( )
A.(-∞,1-
| B.[1-
| C.[1-
| D.(-∞,1+
|
根据题意设x=3+cosθ,y=4+sinθ,
代入不等式得:x-y+c=3+cosθ-4-sinθ+c=cosθ-sinθ-1+c=
cos(θ-
)-1+c≤0恒成立,即c≤1-
cos(θ-
),
∵-1≤cos(θ-
)≤1,
∴1-
≤1-
cos(θ-
)≤1+
,即1-
cos(θ-
)的最小值为1-
,
∴c≤1-
,即c的范围是(-∞,1-
].
故选A
代入不等式得:x-y+c=3+cosθ-4-sinθ+c=cosθ-sinθ-1+c=
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
∵-1≤cos(θ-
| ||
| 2 |
∴1-
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| 2 |
∴c≤1-
| 2 |
| 2 |
故选A

练习册系列答案
相关题目
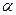 +
+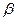 )=1,tan
)=1,tan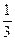 ,则tan
,则tan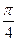 个单位,沿y轴向下平移
个单位,沿y轴向下平移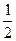 个单位,得到g(x)的图象,已知g(x)的图象关于(
个单位,得到g(x)的图象,已知g(x)的图象关于(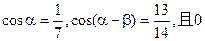 <
<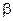 <
<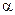 <
<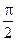 ,
,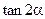 的值.(Ⅱ)求
的值.(Ⅱ)求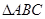 中,若
中,若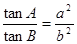 ,则
,则