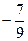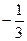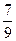题目内容
已知函数f(x)=sin
cos
+cos
sin
+2cos2x-1(x∈R).
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求函数f(x)的单调递增区间.
| 3x |
| 2 |
| x |
| 2 |
| 3x |
| 2 |
| x |
| 2 |
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求函数f(x)的单调递增区间.
(I)f(x)=sin2x+cos2x=
(
sin2x+
cos2x)=
sin(2x+
),
∴T=
=π.
(II)由-
+2kπ≤2x+
≤
+2kπ,解得-
+kπ≤x≤
+kπ(k∈Z).
∴函数f(x)的单调递增区间是[-
+kπ,kπ+
](k∈Z).
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
∴T=
| 2π |
| 2 |
(II)由-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 8 |
| π |
| 8 |
∴函数f(x)的单调递增区间是[-
| 3π |
| 8 |
| π |
| 8 |

练习册系列答案
相关题目
 ,
,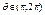 ,求
,求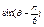 以及
以及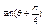 的值.
的值.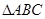 中,已知内角
中,已知内角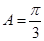 ,边
,边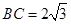 .设内角
.设内角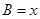 ,面积为
,面积为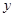 .
.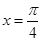 ,求边
,求边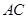 的长;
的长; :
: x
x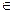 R,
R, 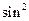
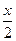 +
+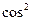
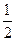
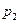 :
: 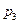 :
: 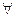 x
x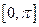 ,
,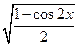 ="sinx "
="sinx " 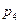 : sinx=cosy
: sinx=cosy x+y=
x+y=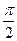
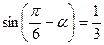 ,则
,则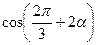 ="( " )
="( " )