Question

【题目】如图，在直四棱柱ABCD－A1B1C1D1中，AD//平面BCC1B1，AD⊥DB.求证：

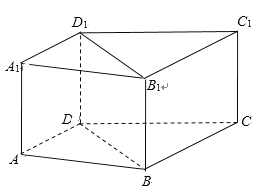
（1）BC//平面ADD1A1；

（2）平面BCC1B1⊥平面BDD1B1.

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

（1）由直线与平面平行的性质可得：由AD//平面BCC1B1，有AD//BC，同时AD平面ADD1A1，可得BC//平面ADD1A1；

（2）由（1）知AD//BC，因为AD⊥DB，所以BC⊥DB，同时由直四棱柱性质可得DD1⊥BC，BC⊥平面BDD1B1，可得证明.

解：（1）因为AD//平面BCC1B1，AD平面ABCD，平面BCC1B1∩平面ABCD=BC，

所以AD//BC.

又因为BC平面ADD1A1，AD平面ADD1A1，

所以BC//平面ADD1A1.

（2）由（1）知AD//BC，因为AD⊥DB，所以BC⊥DB，

在直四棱柱ABCD－A1B1C1D1中DD1⊥平面ABCD，BC底面ABCD，

所以DD1⊥BC，

又因为DD1平面BDD1B1，DB平面BDD1B1，DD1∩DB=D，

所以BC⊥平面BDD1B1，

因为BC平面BCC1B1，

所以平面BCC1B1⊥平面BDD1B1