题目内容
【题目】如图放置的边长为1的正方形![]() 沿
沿![]() 轴滚动(向右为顺时针,向左为逆时针).设顶点
轴滚动(向右为顺时针,向左为逆时针).设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则关于
,则关于![]() 的最小正周期
的最小正周期![]() 及
及![]() 在其两个相邻零点间的图像与x轴所围区域的面积S的正确结论是( )
在其两个相邻零点间的图像与x轴所围区域的面积S的正确结论是( )
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】
从某一个顶点(比如![]() )落在
)落在![]() 轴上的时候开始计算,到下一次
轴上的时候开始计算,到下一次![]() 点落在
点落在![]() 轴上,这个过程中四个顶点依次落在了
轴上,这个过程中四个顶点依次落在了![]() 轴上,而每两个顶点间距离为正方形的边长
轴上,而每两个顶点间距离为正方形的边长![]() ,因此该函数的周期为
,因此该函数的周期为![]() .下面考查点
.下面考查点![]() 的运动轨迹,不妨考查正方形向右滚动,
的运动轨迹,不妨考查正方形向右滚动, ![]() 点从
点从![]() 轴上开始运动的时候,首先是围绕
轴上开始运动的时候,首先是围绕![]() 点运动
点运动![]() 个圆,该圆半径为
个圆,该圆半径为![]() ,然后以
,然后以![]() 点为中心,滚动到
点为中心,滚动到![]() 点落地,其间是以
点落地,其间是以![]() 为半径旋转
为半径旋转![]() ,再以
,再以![]() 为圆心,旋转
为圆心,旋转![]() ,这时候以
,这时候以![]() 为半径,因此最终构成图象如下:
为半径,因此最终构成图象如下:
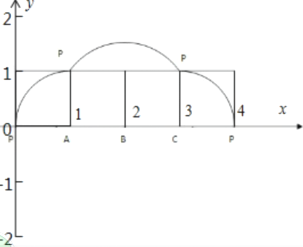
所以两个相邻零点间的图象与![]() 轴所围成区域的面积
轴所围成区域的面积![]() ,故选A.
,故选A.

练习册系列答案
相关题目
【题目】一台机器按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,具有线性相关关系,下表为抽样试验的结果:
转速x(转/秒) | 8 | 10 | 12 | 14 | 16 |
每小时生产有缺点的零件数y(件) | 5 | 7 | 8 | 9 | 11 |
(1)如果y对x有线性相关关系,求回归方程;
(2)若实际生产中,允许每小时生产的产品中有缺点的零件最多有10个,那么机器的运转速度应控制在设么范围内?