Question

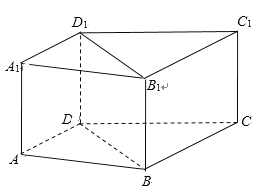
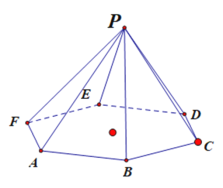
【题目】如图，在正六棱锥中，已知底边为2，侧棱与底面所成角为.

（1）求该六棱锥的体积；

（2）求证：

Answer 1

【答案】（1）12；（2）证明见解析.

【解析】

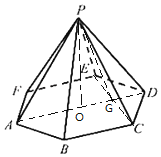
（1）连结AD，过P作PO⊥底面ABCD，交AD于点O，则PA＝2AO＝4，由此能求出该六棱锥的体积．

（2）连结CE，交AD于点O，连结PG，推导出AD⊥CE，PG⊥CE，从而CE⊥平面PAD，由此能证明PA⊥CE．

∵在正六棱锥P﹣ABCDEF中，底边长为2，侧棱与底面所成角为60°．

连结AD，过P作PO⊥底面ABCD，交AD于点O，

则AO＝DO＝2，∠PAO＝60°，∴PA＝2AO＝4，

PO2，

SABCDEF＝6×（）＝6，

∴该六棱锥的体积V12．

（2）连结CE，交AD于点O，连结PG，

∵DE＝CD，AE＝AD，∴AD⊥CE，O是CE中点，

∵PA＝PC，∴PG⊥CE，

∵PG∩AD＝G，∴CE⊥平面PAD，

∵PA平面PAD，∴PA⊥CE．