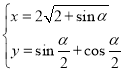题目内容
【题目】已知函数![]() 恰有两个极值点
恰有两个极值点![]() .
.
(1)求实数![]() 的取值范围;
的取值范围;
(2)求证: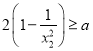 ;
;
(3)求证: ![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
【答案】(1)![]() ;(2)证明见解析;(3)证明见解析.
;(2)证明见解析;(3)证明见解析.
【解析】
(1)求出函数的导数,得到![]() ,设
,设![]() ,求出函数的导数,根据函数的单调性确定
,求出函数的导数,根据函数的单调性确定![]() 的范围即可;
的范围即可;
(2)求出![]() ,问题转化为只要证明
,问题转化为只要证明![]() ,设
,设![]() ,
,![]() ,根据函数的单调性证明即可;
,根据函数的单调性证明即可;
(3)求出![]() ,问题转化为只需证明
,问题转化为只需证明![]() ,根据
,根据![]() ,设
,设![]() ,根据函数的单调性证明即可.
,根据函数的单调性证明即可.
(1)由题意得![]() ,故
,故![]() ,
,
设![]() ,
,![]() ,
,
故![]() 时,
时,![]() 时,
时,![]() ,
,
故![]() 在
在![]() 递增,在
递增,在![]() 递减,
递减,
又![]() ,
,
当![]() 时,
时,![]() ,
,
故实数![]() 的范围是
的范围是![]() ;
;
(2)由(1)得![]() ,且
,且![]() ,故
,故![]() ,
,
要证明![]() ,只要证明
,只要证明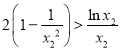 ,
,
只要证明![]() ,
,
设![]() ,
,
则![]() ,
,
故![]() 在
在![]() 递增,
递增,
故![]() ,
,
故![]() 成立;
成立;
(3)由(1)得![]() ,
,
且![]() ,故
,故![]() ,
,
由(1)得![]() ,要证明
,要证明![]() ,
,
只需证明![]() ,
,
只需证明![]() ,
,
故![]()
![]()
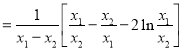 ,
,
设![]() ,
,
则![]() ,
,
故![]() 在
在![]() 递增,
递增,
结合![]() ,故
,故![]() ,
,
![]() ,有
,有![]() ,
,
故![]() ,
,
故![]() .
.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案【题目】《厉害了,我的国》是2018年在我国各影院上映的一部非常火的电影纪录片,该部影片主要讲述了我国近几年的发展现状和成就,影片通过讲述中国故事,刻画中国面貌,弘扬了中国精神,引起了国民的高度关注,上映仅半个月影片票房就突破了3亿元,刷新了我国纪录片的票房纪录,某市一电影院为了解该影院观看《厉害了,我的国》的观众的年龄构成情况,随机抽取了40名观众数据统计如表:
年龄/岁 | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) |
人数 | 6 | 8 | 12 | 6 | 4 | 2 | 2 |
(1)求所调查的40名观众年龄的平均数和中位数;
(2)该电影院决定采用抽奖方式来提升观影人数,将《厉害了,我的国》的电影票票价提高20元/张,并允许购买电影票的观众抽奖3次,中奖1次、2次、3次分别奖现金20元、30元、60元,设观众每次中奖的概率均为![]() ,则观众在3次抽奖中所获得的奖金总额的数学期望是多少元(结果保留整数)?
,则观众在3次抽奖中所获得的奖金总额的数学期望是多少元(结果保留整数)?