题目内容
【题目】已知直线l：x+y-6=0，过直线上一点P作圆x2+y2=4的切线，切点分别为A，B，则四边形PAOB面积的最小值为______，此时四边形PAOB外接圆的方程为______．
【答案】2
（x-
）2+（y-）2=
【解析】
求出O到直线l的最短距离即可得出四边形的最小面积，求出此时P的坐标，得出OP的中点坐标，从而得出外接圆方程．
圆x2+y2=4的半径为2，圆心为（0，0），
由切线性质可知OA⊥AP，
，
又△OAP的面积
，
∴当OP取得最小值时，△OAP的面积取得最小值，
又OP的最小值为O到直线l的距离d=3
．
∴四边形PAOB面积的最小值为：
．
此时，四边形PAOB外接圆直径为d=3．
∵OP⊥直线l，
∴直线OP的方程为x-y=0．
联立方程组，解得P（3，3），
∴OP的中点为
，
∴四边形PAOB外接圆的方程为（x-
）2+（y-）2=
．
故答案为：
，（x-）2+（y-）2=．
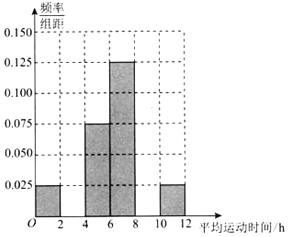
小学教材完全解读系列答案
【题目】已知某企业有职工5000人，其中男职工3500人，女职工1500人．该企业为了丰富职工的业余生活，决定新建职工活动中心，为此，该企业工会采用分层抽样的方法，随机抽取了300名职工每周的平均运动时间（单位：h），汇总得到频率分布表（如表所示），并据此来估计该企业职工每周的运动时间：
平均运动时间 | 频数 | 频率 |
[0，2） | 15 | 0.05 |
[2，4） | m | 0.2 |
[4，6） | 45 | 0.15 |
[6，8） | 755 | 0.25 |
[8，10） | 90 | 0.3 |
[10，12） | p | n |
合计 | 300 | 1 |
（1）求抽取的女职工的人数；
（2）①根据频率分布表，求出m、n、p的值，完成如图所示的频率分布直方图，并估计该企业职工每周的平均运动时间不低于4h的概率；
男职工 | 女职工 | 总计 | |
平均运动时间低于4h | |||
平均运动时间不低于4h | |||
总计 |
②若在样本数据中，有60名女职工每周的平均运动时间不低于4h，请完成以下2×2列联表，并判断是否有95%以上的把握认为“该企业职工毎周的平均运动时间不低于4h与性别有关”．
附：K2=
，其中n=a+b+c+d．
P（K2≥k0） | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
【题目】某学校为了解高一新生的体质健康状况，对学生的体质进行了测试. 现从男、女生中各随机抽取
人，把他们的测试数据，按照《国家学生体质健康标准》整理如下表. 规定：数据≥
，体质健康为合格.
等级 | 数据范围 | 男生人数 | 男生平均分 | 女生人数 | 女生平均分 |
优秀 |
|
|
|
|
|
良好 |
|
|
|
|
|
及格 |
|
|
|
|
|
不及格 |
|
|
|
|
|
总计 | -- |
|
|
|
|
(I)从样本中随机选取一名学生，求这名学生体质健康合格的概率；
(II)从男生样本和女生样本中各随机选取一人，求恰有一人的体质健康等级是优秀的概率；
（III）表中优秀、良好、及格、不及格四个等级的男生、女生平均分都接近（二者之差的绝对值不大于
），但男生的总平均分却明显高于女生的总平均分．研究发现，若去掉四个等级中一个等级的数据，则男生、女生的总平均分也接近，请写出去掉的这个等级．（只需写出结论）
