题目内容
19.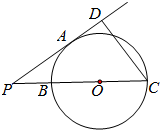 如图,已知PA是圆O的切线,切点为A,PC过圆心O,且与圆O交于B,C两点,过C点作CD⊥PA,垂足为D,PA=4,BC=6,那么CD=$\frac{24}{5}$.
如图,已知PA是圆O的切线,切点为A,PC过圆心O,且与圆O交于B,C两点,过C点作CD⊥PA,垂足为D,PA=4,BC=6,那么CD=$\frac{24}{5}$.
分析 利用切割线定理,求出PO,利用△OAP∽△CDP,求出CD.
解答  解:由题意,利用切割线定理可得:42=PB•(PB+6),
解:由题意,利用切割线定理可得:42=PB•(PB+6),
∴PB=2,
∴PO=5,
连接OA,则OA⊥PA,
∵CD⊥PA,
∴△OAP∽△CDP,
∴$\frac{OA}{CD}=\frac{PO}{PC}$,
∴$\frac{3}{CD}=\frac{5}{8}$
∴CD=$\frac{24}{5}$.
故答案为:$\frac{24}{5}$.
点评 本题考查切割线定理,考查三角形相似的判定与性质,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.要得到函数y=sin2x的图象,只需将函数$y=cos(2x-\frac{π}{3})$的图象( )
| A. | 向右平移$\frac{π}{6}$个单位长度 | B. | 向左平移$\frac{π}{6}$个单位长度 | ||
| C. | 向右平移$\frac{π}{12}$个单位长度 | D. | 向左平移$\frac{π}{12}$个单位长度 |
4.已知{an}是等差数列,a3=5,a9=17,数列{bn}的前n项和Sn=3n,若am=b1+b4,则正整数m等于( )
| A. | 29 | B. | 28 | C. | 27 | D. | 26 |
9.已知集合M={x|2x-x2>0},N={x|x2+y2=1},则M∩N=( )
| A. | [-1,2) | B. | (0,1) | C. | (0,1] | D. | ∅ |
 已知三次函数f(x)=x3+bx2+cx+d的图象如图所示,求f(x)的表达式,并求出f(4)的值.
已知三次函数f(x)=x3+bx2+cx+d的图象如图所示,求f(x)的表达式,并求出f(4)的值.