题目内容
9.已知集合M={x|2x-x2>0},N={x|x2+y2=1},则M∩N=( )| A. | [-1,2) | B. | (0,1) | C. | (0,1] | D. | ∅ |
分析 求出M中不等式的解集确定出M,求出N中x的范围确定出N,找出两集合的交集即可.
解答 解:由M中不等式变形得:x(x-2)<0,
解得:0<x<2,即M=(0,2),
由N中x2+y2=1,得到-1≤x≤1,即N=[-1,1],
∴M∩N=(0,1],
故选:C.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.利用计算机产生0~3之间的均匀随机数a、x,则事件“logax>0(a>0且a≠≠1)”发生的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{9}$ | D. | $\frac{5}{9}$ |
17.高三(3)班共有学生56人,座号分别为1,2,3,…,56,现根据座号,用系统抽样的方法,抽取一个容量为4的样本.已知3号、17号、45号同学在样本中,那么样本中还有一个同学的座号是( )
| A. | 30 | B. | 31 | C. | 32 | D. | 33 |
4.为了分流地铁高峰的压力,某市发改委通过听众会,决定实施低峰优惠票价制度.不超过22公里的地铁票价如下表:
现有甲、乙两位乘客,他们乘坐的里程都不超过22公里.已知甲、乙乘车不超过6公里的概率分别为$\frac{1}{4}$,$\frac{1}{3}$,甲、乙乘车超过6公里且不超过12公里的概率分别为$\frac{1}{2}$,$\frac{1}{3}$.
(Ⅰ)求甲、乙两人所付乘车费用不相同的概率;
(Ⅱ)设甲、乙两人所付乘车费用之和为随机变量ξ,求ξ的分布列与数学期望.
| 乘坐里程x(单位:km) | 0<x≤6 | 6<x≤12 | 12<x≤22 |
| 票价(单位:元) | 3 | 4 | 5 |
(Ⅰ)求甲、乙两人所付乘车费用不相同的概率;
(Ⅱ)设甲、乙两人所付乘车费用之和为随机变量ξ,求ξ的分布列与数学期望.
19.设集合A={x|x-1>0},集合B={x|x≤3},则A∩B=( )
| A. | (-1,3) | B. | (1,3] | C. | [1,3) | D. | [-1,3] |
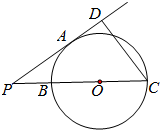 如图,已知PA是圆O的切线,切点为A,PC过圆心O,且与圆O交于B,C两点,过C点作CD⊥PA,垂足为D,PA=4,BC=6,那么CD=$\frac{24}{5}$.
如图,已知PA是圆O的切线,切点为A,PC过圆心O,且与圆O交于B,C两点,过C点作CD⊥PA,垂足为D,PA=4,BC=6,那么CD=$\frac{24}{5}$. 如图,已知AB,CD是外离两圆⊙O1,与⊙O2的外公共切线,切点为A,B,C,求证:A,B,C,D四点共圆.
如图,已知AB,CD是外离两圆⊙O1,与⊙O2的外公共切线,切点为A,B,C,求证:A,B,C,D四点共圆.