题目内容
3.要得到函数y=sin2x的图象,只需将函数$y=cos(2x-\frac{π}{3})$的图象( )| A. | 向右平移$\frac{π}{6}$个单位长度 | B. | 向左平移$\frac{π}{6}$个单位长度 | ||
| C. | 向右平移$\frac{π}{12}$个单位长度 | D. | 向左平移$\frac{π}{12}$个单位长度 |
分析 利用诱导公式化简函数y=cos(2x-$\frac{π}{3}$)为正弦函数类型,然后通过平移原则,推出选项.
解答 解:因为函数y=cos(2x-$\frac{π}{3}$)=sin(2x+$\frac{π}{6}$),
所以可将函数y=cos(2x-$\frac{π}{3}$)的图象,沿x轴向右平移$\frac{π}{12}$,得到y=sin[2(x-$\frac{π}{12}$)+$\frac{π}{6}$]=sin2x,得到函数y=sin2x的图象,
故选:C.
点评 本题考查三角函数的诱导公式的应用,函数的图象的平移,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,则f(1)=( )


| A. | -$\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
8.将函数y=sin(2x+θ)的图象向右平移$\frac{π}{6}$个单位,得到的图象关于y轴对称,则θ的一个可能的值为( )
| A. | $\frac{π}{6}$ | B. | $-\frac{π}{6}$ | C. | $-\frac{π}{3}$ | D. | $-\frac{2π}{3}$ ( |
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,∠ABC=∠ADC=90°,CB=CD=1,∠BCD=120°,E为线段BP的靠近点B的一个四等分点,AE⊥PC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,∠ABC=∠ADC=90°,CB=CD=1,∠BCD=120°,E为线段BP的靠近点B的一个四等分点,AE⊥PC.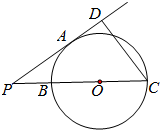 如图,已知PA是圆O的切线,切点为A,PC过圆心O,且与圆O交于B,C两点,过C点作CD⊥PA,垂足为D,PA=4,BC=6,那么CD=$\frac{24}{5}$.
如图,已知PA是圆O的切线,切点为A,PC过圆心O,且与圆O交于B,C两点,过C点作CD⊥PA,垂足为D,PA=4,BC=6,那么CD=$\frac{24}{5}$.