题目内容
11.设函数f(x)=x2-(a-2)x-alnx.(I)求函数f(x)的单调区间;
(Ⅱ)若方程f(x)=c(c∈R),有两个不相等的实数根x1、x2,求证:$f'(\frac{{{x_1}+{x_2}}}{2})>0$.
分析 (I)求出函数的导数通过当a≤0时,当a>0时,判断导函数的符号,推出函数的单调区间.
(II)通过x1、x2是方程f(x)=c的两个不等实根,由(1)知a>0.设0<x1<x2,把根代入方程,作差,推出a的表达式,构造函数,利用新函数的导数,通过函数的单调性利用分析法证明即可.
解答 (12分)
解:(I) f′(x)=2x-(a-2)-$\frac{a}{x}=\frac{{2{x^2}-(a-2)x-a}}{x}=\frac{(2x-a)(x+1)}{x}$(x>0).
当a≤0时,f′(x)>0,函数f(x)在(0,+∞)上单调递增,函数f(x)的单调增区间为(0,+∞).
当a>0时,由f′(x)>0,得x>$\frac{a}{2}$;由f′(x)<0,得0<x<$\frac{a}{2}$.
所以函数f(x)的单调增区间为$({\frac{a}{2},+∞})$,单调减区间为$({0,\frac{a}{2}})$.…(4分)
(II)证明:因为x1、x2是方程f(x)=c的两个不等实根,由(1)知a>0.
不妨设0<x1<x2,则$x_1^2$-(a-2)x1-alnx1=c,$x_2^2$-(a-2)x2-alnx2=c.
两式相减得$x_1^2$-(a-2)x1-alnx1-$x_2^2$+(a-2)•x2+alnx2=0,
即$x_1^2$+2x1-$x_2^2$-2x2=ax1+alnx1-ax2-alnx2=a(x1+lnx1-x2-lnx2).
所以a=$\frac{{x_1^2+2{x_1}-x_2^2-2{x_2}}}{{{x_1}+ln{x_1}-{x_2}-ln{x_2}}}$.因为f′$({\frac{a}{2}})$=0,
当x∈$({0,\frac{a}{2}})$时,f′(x)<0,当x∈$({\frac{a}{2},+∞})$时,f′(x)>0,
故只要证$({\frac{{{x_1}+{x_2}}}{2}})$>$\frac{a}{2}$即可,即证明x1+x2>$\frac{{x_1^2+2{x_1}-x_2^2-2{x_2}}}{{{x_1}+ln{x_1}-{x_2}-ln{x_2}}}$,
即证明$x_1^2$-$x_2^2$+(x1+x2)(lnx1-lnx2)<$x_1^2$+2x1-$x_2^2$-2x2,
即证明ln $\frac{x_1}{x_2}$<$\frac{{2{x_1}-2{x_2}}}{{{x_1}+{x_2}}}$.设t=$\frac{x_1}{x_2}$(0<t<1).
令g(t)=lnt-$\frac{2t-2}{t+1}$,则g′(t)=$\frac{1}{t}-\frac{4}{{(t+1{)^2}}}=\frac{{(t-1{)^2}}}{{t(t+1{)^2}}}$.
因为t>0,所以g′(t)≥0,当且仅当t=1时,g′(t)=0,所以g(t)在(0,+∞)上是增函数.
又g(1)=0,所以当t∈(0,1)时,g(t)<0总成立.所以原题得证 …(12分)
点评 本题考查函数的导数的综合应用,函数的单调性,分类讨论思想的应用,构造法的应用,考查分析问题解决问题的能力.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案| A. | {0,1,2} | B. | {0,1} | C. | {x|0<x<2} | D. | {x|-3<x<2} |
| A. | $\frac{2}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{9}$ | D. | $\frac{5}{9}$ |
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,∠ABC=∠ADC=90°,CB=CD=1,∠BCD=120°,E为线段BP的靠近点B的一个四等分点,AE⊥PC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,∠ABC=∠ADC=90°,CB=CD=1,∠BCD=120°,E为线段BP的靠近点B的一个四等分点,AE⊥PC.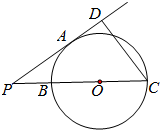 如图,已知PA是圆O的切线,切点为A,PC过圆心O,且与圆O交于B,C两点,过C点作CD⊥PA,垂足为D,PA=4,BC=6,那么CD=$\frac{24}{5}$.
如图,已知PA是圆O的切线,切点为A,PC过圆心O,且与圆O交于B,C两点,过C点作CD⊥PA,垂足为D,PA=4,BC=6,那么CD=$\frac{24}{5}$. 如图,已知AB,CD是外离两圆⊙O1,与⊙O2的外公共切线,切点为A,B,C,求证:A,B,C,D四点共圆.
如图,已知AB,CD是外离两圆⊙O1,与⊙O2的外公共切线,切点为A,B,C,求证:A,B,C,D四点共圆.