题目内容
【题目】已知抛物线
的焦点为
，平行于
轴的两条直线
分别交
于
两点，交
的准线于
两点.
(1)若
在线段
上， 
是
的中点，证明： 
；
(2)若
的面积是
的面积的两倍，求
中点的轨迹方程.
【答案】(1)证明见解析；(2) 
.
【解析】试题分析：（1）设出与
轴平行的两条直线，然后得出
， 
， 
， 
， 
的坐标，然后通过证明直线
与直线
的斜率相等即可证明结果；（2）设
与
轴的交点为
，利用面积可求得
，设
的中点为
，根据
与
轴是否垂直分两种情况，结合
求解.
试题解析：由题知
，设
： 
， 
： 
，则
，且
， 
， 
， 
， 
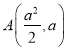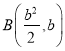，记过
， 
两点的直线为
，则
的方程为
(1)由于
在线段
上，故
，
记
的斜率为
， 
的斜率为
，则
，
∴
.
(2)设
与
轴的交点为
，
则
， 
，
由题设得
，所以
(舍)， 
.
设满足条件的
的中点为
当
与
轴不垂直时，由
可得
而
，所以
，
当
与
轴垂直时， 
与
重合
所以，所求轨迹方程为
.
阅读快车系列答案【题目】某个体经营者把开始六个月试销A、B两种商品的逐月投资与所获纯利润列成下表：
投资A商品金额（万元） | 1 | 2 | 3 | 4 | 5 | 6 |
获纯利润（万元） | 0.65 | 1.39 | 1.85 | 2 | 1.84 | 1.40 |
投资B商品金额（万元） | 1 | 2 | 3 | 4 | 5 | 6 |
获纯利润（万元） | 0.25 | 0.49 | 0.76 | 1 | 1.26 | 1.51 |
该经营者准备下月投入12万元经营这两种产品，但不知投入A、B两种商品各多少才最合算．请你帮助制定一下资金投入方案，使得该经营者能获得最大利润，并按你的方案求出该经营者下月可获得的最大利润（结果保留两个有效数字）．
【题目】某地区居民生活用电分为高峰和低谷两个时间段进行分时计价．该地区的电网销售电价表如下：
高峰时间段用电价格表 | 低谷时间段用电价格表 | ||
高峰月用 电量(单 位：千瓦时) | 高峰电价 (单位：元/ 千瓦时) | 低谷月用 电量(单位： 千瓦时) | 低谷电价 (单位：元/ 千瓦时) |
50及以下 的部分 | 0.568 | 50及以下 的部分 | 0.288 |
超过 50 至 200 的部分 | 0.598 | 超过 50 至 200 的部分 | 0.318 |
超过200 的部分 | 0.668 | 超过 200 的部分 | 0.388 |
若某家庭5月份的高峰时间段用电量为 200 千瓦时，低谷时间段用电量为 100 千瓦时，则按这种计费方式该家庭本月应付的电费为____________元．(用数字作答)
