Question

【题目】已知函数．

（Ⅰ）求函数的单调区间；

（Ⅱ）若时恒成立，求实数的取值范围．

Answer 1

【答案】（Ⅰ）见解析;（Ⅱ）.

【解析】试题分析：（Ⅰ）分情况讨论的范围，求出，分别令求得的范围，可得函数增区间， 求得的范围，可得函数的减区间；（Ⅱ） 恒成立， 恒成立，令，分三种情况讨论的范围，分别利用导数讨论函数的单调性，求出最小值，筛选出符合题意的实数的取值范围即可.

试题解析：（Ⅰ）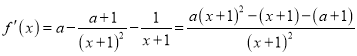

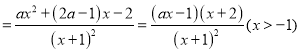
当时， 在上递增，在上递减；

当时， 在上递减；

当时， 在上递减，在上递增．

（Ⅱ）即恒成立

令

令，

（1）当时， ，函数在上单调递增，

因为，所以， 时， ，符合题意；

（2）当 时， ，方程有两不等式根，

又且对称轴 ，可得

所以，函数在上单调递增，

又，所以， 时， ，符合题意；

（3）当 时，由 ，可得

所以 时，函数 单调递减；

又

所以，当时， 不符合题意；

综上所述， 的取值范围是