题目内容
【题目】已知函数![]()
(1)求函数![]() 的定义域;
的定义域;
(2)判断函数![]() 的奇偶性。
的奇偶性。
【答案】(1){x|﹣1<x<1}(2)偶函数
【解析】
(1)要求函数f(x)+g(x)的定义域,我们可根据让函数解析式有意义的原则,构造不等式组,解不等式组即可得到函数f(x)+g(x)的定义域;
(2)要判断h(x)=f(x)+g(x)的奇偶性,我们根据奇偶性的定义,先判断其定义域是否关于原点对称,然后再判断f(﹣x)+g(﹣x)与f(x)+g(x)的关系,结合奇偶性的定义进行判断;
(1)f(x)+g(x)=![]() +
+![]() .
.
若要上式有意义,则![]() ,
,
即﹣1<x<1.
所以所求定义域为{x|﹣1<x<1}
(2)记h(x)=f(x)+g(x),定义域为{x|﹣1<x<1}
则h(﹣x)=f(﹣x)+g(﹣x)
=log2(﹣x+1)+log2(1+x)=h(x).
所以h(x)=f(x)+g(x)是偶函数.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
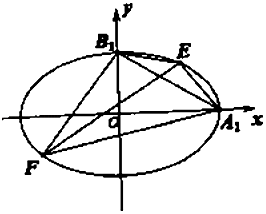
【题目】如图,设椭圆的中心为原点![]() ,长轴在
,长轴在![]() 轴上,上顶点为
轴上,上顶点为![]() ,左,右焦点分别为
,左,右焦点分别为![]() ,线段
,线段![]() 的中点分别为
的中点分别为![]() ,且
,且![]() 是面积为4的直角三角形.
是面积为4的直角三角形.
(1)求该椭圆的离心率和标准方程;
(2)过![]() 做直线
做直线![]() 交椭圆于
交椭圆于![]() 两点,使
两点,使![]() ,求直线
,求直线![]() 的方程.
的方程.

【题目】某个体经营者把开始六个月试销A、B两种商品的逐月投资与所获纯利润列成下表:
投资A商品金额(万元) | 1 | 2 | 3 | 4 | 5 | 6 |
获纯利润(万元) | 0.65 | 1.39 | 1.85 | 2 | 1.84 | 1.40 |
投资B商品金额(万元) | 1 | 2 | 3 | 4 | 5 | 6 |
获纯利润(万元) | 0.25 | 0.49 | 0.76 | 1 | 1.26 | 1.51 |
该经营者准备下月投入12万元经营这两种产品,但不知投入A、B两种商品各多少才最合算.请你帮助制定一下资金投入方案,使得该经营者能获得最大利润,并按你的方案求出该经营者下月可获得的最大利润(结果保留两个有效数字).