Question

【题目】已知椭圆C： =1（a＞b＞0）的焦点分别为 、 ，点P在椭圆C上，满足|PF1|=7|PF2|，tan∠F1PF2=4 ．
（Ⅰ）求椭圆C的方程；
（Ⅱ）已知点A（1，0），试探究是否存在直线l：y=kx+m与椭圆C交于D、E两点，且使得|AD|=|AE|？若存在，求出k的取值范围；若不存在，请说明理由．

Answer 1

【答案】解：（I）∵tan∠F1PF2=4 ．∴cos∠F1PF2= ．设|PF1|=m，|PF2|=n，∵|PF1|=7|PF2|，∴m=7n．
联立 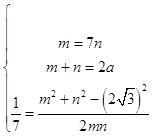，解得a=2，m= ，n= ．
∴b2=a2﹣c2=1，
故所求C的方程为 ．
（II）假设存在直线l满足题设，设D（x1 ， y1），E（x2 ， y2），
将y=kx+m代入 并整理得（1+4k2）x2+8kmx+4m2﹣4=0，
由△=64k2m2﹣4（1+4k2）（4m2﹣4）=﹣16（m2﹣4k2﹣1）＞0，
得4k2+1＞m2 ， ①
又 ，
设D，E中点为M（x0 ， y0），M ，
∵kAMk=﹣1，得② ，
将②代入①得 ，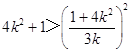
化简得20k4+k2﹣1＞0（4k2+1）（5k2﹣1）＞0，解得 或
∴存在直线l，使得|AD|=|AE|，此时k的取值范围为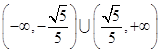
【解析】（Ⅰ）由tan∠F1PF2=4 ．可得cos∠F1PF2= ．设|PF1|=m，|PF2|=n，由|PF1|=7|PF2|，可得m=7n．
利用椭圆的定义及其余弦定理可得 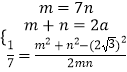，解得即可得出．（II）假设存在直线l满足题设，设D（x1 ， y1），E（x2 ， y2），将y=kx+m代入椭圆方程可得：（1+4k2）x2+8kmx+4m2﹣4=0，由于△＞0，可得4k2+1＞m2 ， 设D，E中点为M（x0 ， y0），利用根与系数的关系可得： ，利用kAMk=﹣1，得 ，代入△＞0解出即可．