题目内容
【题目】已知单调递增的等比数列{an}满足：a2+a3+a4=28，且a3+2是a2 ， a4的等差中项．
（1）求数列{an}的通项公式
（2）若bn=anlog 
an ， Sn=b1+b2+b3+…+bn ， 对任意正整数n，Sn+（n+m）an+1＜0恒成立，试求m的取值范围．
【答案】
（1）解：设等比数列{an}的首项为a1，公比为q．
依题意，
有2（a3+2）=a2+a4，
代入a2+a3+a4=28，
得a3=8．
∴a2+a4=20．
∴ 
解之得 
，或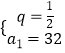 
又{an}单调递增，
∴q=2，a1=2，∴an=2n，
（2）解：bn=2nlog 
2n=﹣n2n，
∴﹣Sn=1×2+2×22+3×23++n×2n①
﹣2Sn=1×22+2×23++（n﹣1）2n+n2n+1②
①﹣②得，Sn=2+22+23++2n﹣n2n+1
= 
﹣n2n+1
=2n+1﹣2﹣n2n+1
由Sn+（n+m）an+1＜0，
即2n+1﹣2﹣n2n+1+n2n+1+m2n+1＜0对任意正整数n恒成立，
∴m2n+1＜2﹣2n+1．
对任意正整数n，
m＜ 
﹣1恒成立．
∵ ﹣1＞﹣1，∴m≤﹣1．
即m的取值范围是（﹣∞，﹣1]．
【解析】（1）设等比数列{an}的首项为a1 ， 公比为q，根据2（a3+2）=a2+a4 ， 可求得a3 ． 进而求得a2+a4=20．两式联立方程即可求得a1和q的值，最后根据等比数列的通项公式求得an ． （2）把（1）中的an代入bn ， 再利用错位相减法求得Sn ， 再由Sn+（n+m）an+1＜0恒成立进而求得m的范围．
【考点精析】解答此题的关键在于理解等比数列的基本性质的相关知识，掌握{an}为等比数列，则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列，以及对数列的通项公式的理解，了解如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
