题目内容
为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取12件和5件,测量产品中微量元素x,y的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 76 | 81 |
(2)当产品中的微量元素x,y满足x≥175且y≥75,该产品为优等品,
①用上述样本数据估计乙厂生产的优等品的数量;
②从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数
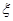 的分布列及其期望.
的分布列及其期望.
(I)35 ;(II)①21件; ②所以随机变量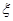 的分布列为
的分布列为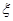
0 1 2 
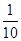
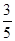
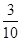
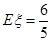 .
.
解析试题分析:(I)根据分层抽样的特点:每层按比例抽样,即各层样本数与该层总体数的比值相等,可得到乙厂产品数量.(II)①,根据列表统计优等品的频数,根据频数与容量之比=频率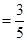 ,易知乙厂优等品数量21件。②根据简单随机抽样中随机变量的分布,确定
,易知乙厂优等品数量21件。②根据简单随机抽样中随机变量的分布,确定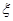 的可能取值情况,再列出随机变量的分布列易求均值.
的可能取值情况,再列出随机变量的分布列易求均值.
试题解析:(I)设乙厂生产的产品数量为x件,由题意得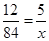 ,所以
,所以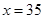 ;
;
(II)①由题意知乙厂生产的优等品的数量为 件;②由题意知乙厂抽取的5件产品中共有3件优等品,随机抽取两件,易知随机变量
件;②由题意知乙厂抽取的5件产品中共有3件优等品,随机抽取两件,易知随机变量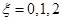 ,
,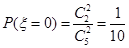 ,
,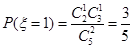 ,
, ,所以随机变量
,所以随机变量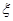 的分布列为
的分布列为
0 1 2 
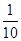
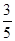
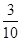
所以随机变量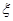 的期望
的期望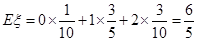 .
.
考点:1、分层抽样的性质和公式 2、简单随机变量的分布列及均值.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
某大学一个专业团队为某专业大学生研究了多款学习软件,其中有A、B、C三种软件投入使用,经一学年使用后,团队调查了这个专业大一四个班的使用情况,从各班抽取的样本人数如下表
| 班级 | 一 | 二 | 三 | 四 |
| 人数 | 3 | 2 | 3 | 4 |
(2)从这12名学生中,指定甲、乙、丙三人为代表,已知他们下午自习时间每人选择A、B两个软件学习的概率每个都是
 ,且他们选择A、B、C任一款软件都是相互独立的.设这三名学生中下午自习时间选软件C的人数为
,且他们选择A、B、C任一款软件都是相互独立的.设这三名学生中下午自习时间选软件C的人数为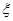 ,求
,求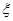 的分布列和数学期望.
的分布列和数学期望. 已知某校在一次考试中,5名学生的数学和物理成绩如下表:
| 学生的编号i | 1 | 2 | 3 | 4 | 5 |
| 数学成绩x | 80 | 75 | 70 | 65 | 60 |
| 物理成绩y | 70 | 66 | 68 | 64 | 62 |
(Ⅱ)根据上表,利用最小二乘法,求出
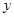 关于
关于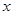 的线性回归方程
的线性回归方程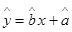 ,
,其中
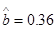
(III)利用(Ⅱ)中的线性回归方程,试估计数学90分的同学的物理成绩.(四舍五入到整数)
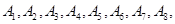 (如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为
(如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为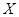 .若
.若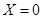 就参加学校合唱团,否则就参加学校排球队.
就参加学校合唱团,否则就参加学校排球队.


 •
•
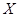 位,若连续抽取到两位愿意购买本地家禽的市民,或抽取的人数达到4位,则停止抽取,求
位,若连续抽取到两位愿意购买本地家禽的市民,或抽取的人数达到4位,则停止抽取,求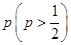 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为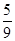 .
.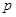 的值;
的值;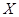 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量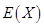 .
.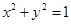 相切的概率;
相切的概率;