题目内容
今年我国部分省市出现了人感染H7N9禽流感确诊病例,各地家禽市场受其影响生意冷清.A市虽未发现H7N9疑似病例,但经抽样有20%的市民表示还会购买本地家禽.现将频率视为概率,解决下列问题:
(Ⅰ)从该市市民中随机抽取3位,求至少有一位市民还会购买本地家禽的概率;
(Ⅱ)从该市市民中随机抽取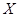 位,若连续抽取到两位愿意购买本地家禽的市民,或抽取的人数达到4位,则停止抽取,求
位,若连续抽取到两位愿意购买本地家禽的市民,或抽取的人数达到4位,则停止抽取,求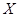 的分布列及数学期望.
的分布列及数学期望.
(Ⅰ)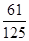 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
解析试题分析:(Ⅰ)利用事件“该市市民中随机抽取3位,至少有一位市民还会购买本地家禽”的对立事件“该市市民中随机抽取3位,没有一位市民会购买本地家禽”,对立事件只有一种情况,而事件本身有3种基本情况,这样就方便了计算,算出对立事件的概率后,再根据对立事件与原事件的概率之和为1即可求出原事件的概率;(Ⅱ)先把随机变量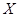 的可能值列出来,然后按照相应的
的可能值列出来,然后按照相应的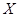 值利用排列组合的相关知识求对应的概率,列出相应的概率分布列进行计算即可.
值利用排列组合的相关知识求对应的概率,列出相应的概率分布列进行计算即可.
试题解析:(Ⅰ)依题意可得,任意抽取一位市民会购买本地家禽的概率为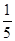 ,
,
从而任意抽取一位市民不会购买本地家禽的概率为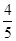 .
.
设“至少有一位市民会购买本地家禽”为事件 ,则
,则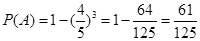 ,
,
故至少有一位市民会购买本地家禽的概率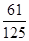 . 6分
. 6分
(Ⅱ)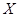 的所有可能取值为:2,3,4.
的所有可能取值为:2,3,4. ,
,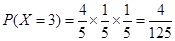 ,
,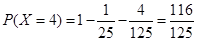 ,
,
所以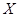 的分布列为:
的分布列为: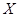
2 3 4 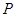
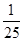
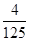
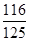
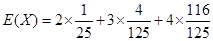
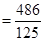 . 13分
. 13分
考点:二项分布、离散型随机变量的分布列与数学期望

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取12件和5件,测量产品中微量元素x,y的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 76 | 81 |
(2)当产品中的微量元素x,y满足x≥175且y≥75,该产品为优等品,
①用上述样本数据估计乙厂生产的优等品的数量;
②从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数
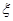 的分布列及其期望.
的分布列及其期望. 某经销商试销A、B两种商品一个月(30天)的记录如下:
| 日销售量(件) | 0 | 1 | 2 | 3 | 4 | 5 |
| 商品A的频数 | 3 | 5 | 7 | 7 | 5 | 3 |
| 商品B的频数 | 4 | 4 | 6 | 8 | 5 | 3 |
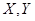 表示售出A、B商品的日利润值(单位:元).将频率视为概率.
表示售出A、B商品的日利润值(单位:元).将频率视为概率.(Ⅰ)设两种商品的销售量互不影响,求两种商品日获利值均超过100元的概率;
(Ⅱ)由于某种原因,该商家决定只选择经销A、B商品的一种,你认为应选择哪种商品,说明理由.
某小组共有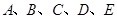 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)
五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)
如下表所示:
| | A | B | C | D | E |
| 身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
| 体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
(Ⅰ)从该小组身高低于
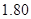 的同学中任选
的同学中任选 人,求选到的
人,求选到的 人身高都在
人身高都在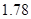 以下的概率
以下的概率(Ⅱ)从该小组同学中任选
 人,求选到的
人,求选到的 人的身高都在
人的身高都在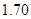 以上且体重指标都在
以上且体重指标都在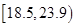 中的概率.
中的概率. 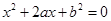 .
.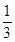 ,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.
,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.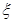 ,求
,求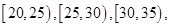
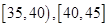 .
. 的值并根据频率分布直方图估计这500名志愿者中年龄在
的值并根据频率分布直方图估计这500名志愿者中年龄在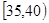 岁的人数;
岁的人数;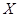 ,求
,求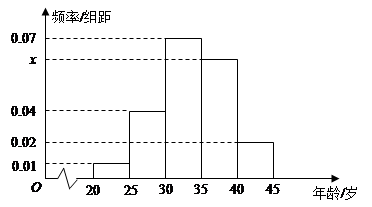
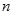 层第
层第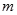 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为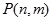 ,某研究性学习小组经探究发现小弹子落入第
,某研究性学习小组经探究发现小弹子落入第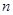 层的第
层的第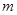 个通道的次数服从二项分布,请你解决下列问题.
个通道的次数服从二项分布,请你解决下列问题.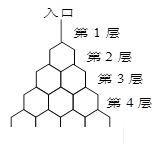
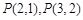 及
及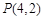 的值,并猜想
的值,并猜想 ,其中
,其中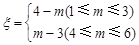 ,试求
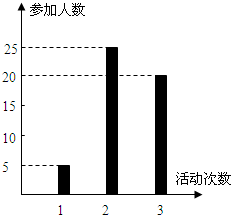
,试求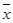 ;(II)从该班中任意选两名学生,求他们参加活动次数恰好相等的概率
;(II)从该班中任意选两名学生,求他们参加活动次数恰好相等的概率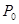 .
.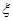 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量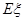 .
.