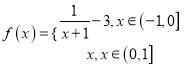题目内容
【题目】设A是同时符合以下性质的函数f(x)组成的集合:
①x∈[0,+∞),都有f(x)∈(1,4];②f(x)在[0,+∞)上是减函数.
(1)判断函数f1(x)=2-![]() 和f2(x)=1+3·
和f2(x)=1+3·![]() (x≥0)是否属于集合A,并简要说明理由;
(x≥0)是否属于集合A,并简要说明理由;
(2)把(1)中你认为是集合A中的一个函数记为g(x),若不等式g(x)+g(x+2)≤k对任意的x≥0总成立,求实数k的取值范围.
【答案】(1)答案见解析;(2) ![]() .
.
【解析】试题分析:
(1)由函数的解析式可得函数![]() 的满足
的满足![]() ,则该函数不在集合A中,考查函数
,则该函数不在集合A中,考查函数![]() 的性质可得函数
的性质可得函数![]() 在集合A中;
在集合A中;
(2)结合(1)的结论可得![]() ,结合函数的解析式可得实数
,结合函数的解析式可得实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(1)f1(x)=2-![]() 不在集合中,f2(x)=1+3·
不在集合中,f2(x)=1+3·![]() x在集合A中,
x在集合A中,
理由:f1(x)=2-![]() ,∵
,∵![]() ≥0,
≥0,
∴2-![]() ≤2,
≤2,
∴f1(x)不在集合A中.
又∵x≥0时,0<![]() x≤1,
x≤1,
∴1<1+3·![]() x≤4,
x≤4,
即f2(x)∈(1,4],
又函数y=![]() x在[0,+∞)是减函数,
x在[0,+∞)是减函数,
∴f2(x)=1+3·![]() x在[0,+∞)也是减函数.
x在[0,+∞)也是减函数.
(2)由(1)知g(x)=1+3·![]() x,
x,
故F(x)=g(x)+g(x+2)=1+3·![]() x+1+3·
x+1+3·![]() x+2=2+
x+2=2+![]() ·
·![]() x.
x.
因为当x≥0时,0<![]() x≤1,
x≤1,
∴2<2+![]() ·
·![]() x≤
x≤![]() ,
,
∴k≥![]() .
.
故k的取值范围为![]() .
.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目