题目内容
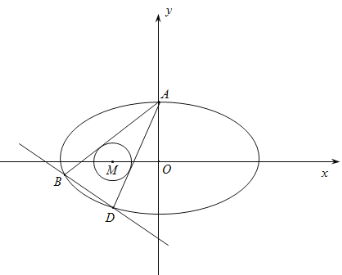
【题目】如图,已知椭圆C:![]() (
(![]() )的上顶点为
)的上顶点为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆C的方程;
(2)若过点A作圆![]() (圆
(圆![]() 在椭圆C内)的两条切线分别与椭圆C相交于B,D两点(B,D不同于点A),当r变化时,试问直线BD是否过某个定点?若是,求出该定点;若不是,请说明理由.
在椭圆C内)的两条切线分别与椭圆C相交于B,D两点(B,D不同于点A),当r变化时,试问直线BD是否过某个定点?若是,求出该定点;若不是,请说明理由.
【答案】(1)![]() ;(2)过定点,
;(2)过定点,![]()
【解析】
(1)根据椭圆的顶点和离心率建立方程组求解椭圆方程;
(2)圆M过A的切线方程可设为l:![]() ,代入椭圆,解出B,D坐标,根据直线与圆相切结合韦达定理得斜率
,代入椭圆,解出B,D坐标,根据直线与圆相切结合韦达定理得斜率![]() 的关系,表示出直线BD的方程即可求得过定点.
的关系,表示出直线BD的方程即可求得过定点.
解:(1)依题意可得: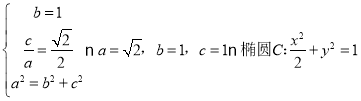 )
)
(2)圆M过A的切线方程可设为l:![]() ,代入椭圆C的方程得:
,代入椭圆C的方程得:
![]() ,
,
可得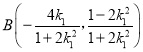 ;同理可得
;同理可得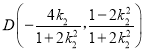
由圆M与l相切得: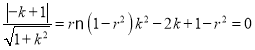
由韦达定理得:![]()
所以直线BD的斜率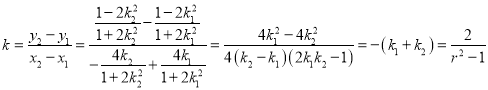 ……
……
直线BD的方程为: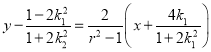
化简为:![]() ,即
,即![]()
所以,当![]() 变化时,直线BD总过定点
变化时,直线BD总过定点![]()

练习册系列答案
相关题目
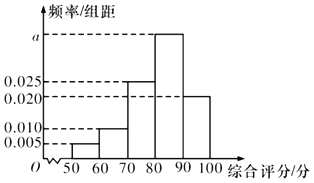
【题目】某种产品的质量用其质量指标值来衡量)质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
![]() 配方的频数分布表:
配方的频数分布表:
指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110] |
频数 | 8 | 20 | 42 | 22 | 8 |
![]() 配方的频数分布表:
配方的频数分布表:
指标值分组 | [90,94) | [94,98) | [98,102) | [102,106] | [106,110] |
频数 | 4 | 12 | 42 | 32 | 10 |
(1)分别估计用![]() 配方、
配方、![]() 配方生产的产品的优质品率;
配方生产的产品的优质品率;
(2)已知用![]() 配方生产的一件产品的利润(单位:元)与其质量指标值
配方生产的一件产品的利润(单位:元)与其质量指标值![]() 的关系为
的关系为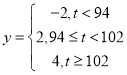 ,估计用
,估计用![]() 配方生产的一件产品的利润大于
配方生产的一件产品的利润大于![]() 的概率,并求用
的概率,并求用![]() 配方生产的上述
配方生产的上述![]() 件产品的平均利润.
件产品的平均利润.