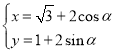题目内容
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程,并说明它是何种曲线;
的直角坐标方程,并说明它是何种曲线;
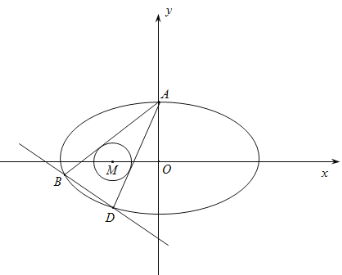
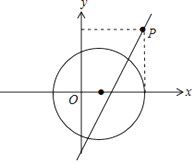
(2)设点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点,求
两点,求![]() 的最大值.
的最大值.
【答案】(1)![]() ,圆;(2)
,圆;(2)![]() .
.
【解析】
(1)将![]() ,
,![]() 代入
代入![]() ,即可得到曲线
,即可得到曲线![]() 的直角坐标方程,并由此判断曲线类型;
的直角坐标方程,并由此判断曲线类型;
(2)由直线![]() 的参数方程,可知直线过定点
的参数方程,可知直线过定点![]() ,将直线
,将直线![]() 的参数方程与曲线
的参数方程与曲线![]() 的直角坐标方程联立,可得到关于
的直角坐标方程联立,可得到关于![]() 的一元二次方程,利用根与系数的关系及
的一元二次方程,利用根与系数的关系及![]() 的几何意义,可求
的几何意义,可求![]() 的最大值.
的最大值.
(1)解:将![]() ,
,![]() ,代入
,代入![]() ,
,
得![]() ,即
,即![]() ,
,
曲线![]() 是以
是以![]() 为圆心,以2为半径的圆;
为圆心,以2为半径的圆;
(2)由直线![]() 的参数方程,可知直线过定点
的参数方程,可知直线过定点![]() ,
,
记![]() ,
,![]() 分别为直线
分别为直线![]() 上
上![]() 、
、![]() 两点对应的参数,
两点对应的参数,
![]() 点
点![]() ,
,![]() 均在点
均在点![]() 的下方,
的下方,
![]()
![]() ,
,![]() ,
,
把![]() ,(
,(![]() 为参数)代入
为参数)代入![]() ,
,
得![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,
令![]() ,得
,得![]() 或
或![]() (舍),
(舍),
由系数![]() 的几何意义知,
的几何意义知,
![]() ,(
,(![]() ),
),
![]()
![]() ,
,
![]()
![]() 的最大值为
的最大值为![]() .
.

【题目】已知某保险公司的某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | ≥4 |
保费(元) |
|
|
|
|
|
随机调查了该险种的![]() 名续保人在一年内的出险情况,得到下表:
名续保人在一年内的出险情况,得到下表:
出险次数 | 0 | 1 | 2 | 3 | ≥4 |
频数 | 280 | 80 | 24 | 12 | 4 |
该保险公司这种保险的赔付规定如下:
出险序次 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次及以上 |
赔付金额(元) |
|
|
|
|
|
将所抽样本的频率视为概率.
(1)求本年度续保人保费的平均值的估计值;
(2)按保险合同规定,若续保人在本年度内出险![]() 次,则可获得赔付
次,则可获得赔付![]() 元;依此类推,求本年度续保人所获赔付金额的平均值的估计值;
元;依此类推,求本年度续保人所获赔付金额的平均值的估计值;
(3)续保人原定约了保险公司的销售人员在上午![]() 之间上门签合同,因为续保人临时有事,外出的时间在上午
之间上门签合同,因为续保人临时有事,外出的时间在上午![]() 之间,请问续保人在离开前见到销售人员的概率是多少?
之间,请问续保人在离开前见到销售人员的概率是多少?
【题目】低碳经济时代,文化和旅游两大产业逐渐成为我国优先发展的“绿色朝阳产业”.为了解某市的旅游业发展情况,某研究机构对该市2019年游客的消费情况进行随机调查,得到频数分布表及频率分布直方图.
旅游消费(千元) |
|
|
|
|
频数(人) | 10 | 60 |
|
|
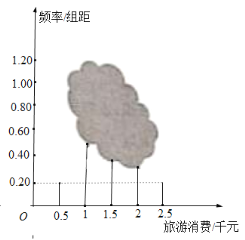
(1)由图表中数据,求![]() 的值及游客人均消费估计值(同一组中的数据以这组数据所在区间中点的值为代表)
的值及游客人均消费估计值(同一组中的数据以这组数据所在区间中点的值为代表)
(2)该机构利用最小二乘法得到2013~2017年该市的年旅游人次![]() (千万人次)与年份代码
(千万人次)与年份代码![]() 的线性回归模型:
的线性回归模型:![]() .
.
注:年份代码1~5分别对应年份2013~2017
①试求2013~2017年的年旅游人次的平均值;
②据统计,2018年该市的年旅游人次为9千万人次.建立2013~2018年该市年旅游人次![]() (千万人次)与年份代码
(千万人次)与年份代码![]() 的线性回归方程,并估计2019年该市的年旅游收入.
的线性回归方程,并估计2019年该市的年旅游收入.
注:年旅游收入=年旅游人次×人均消费
参考数据:![]() .参考公式:
.参考公式: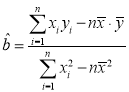 ,
,![]() .
.
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
18 | |||
合计 |
(2)为吸引游客,该超市推出一种优惠方案,购买金额不少于60元可抽奖3次,每次中奖概率为![]() (每次抽奖互不影响,且
(每次抽奖互不影响,且![]() 的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数
的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数![]() (元)的分布列并求其数学期望.
(元)的分布列并求其数学期望.
附:参考公式和数据: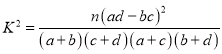 ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |