题目内容
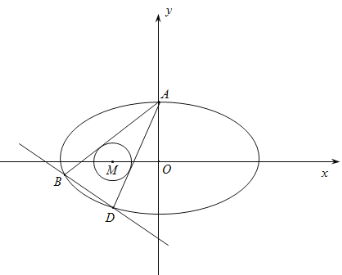
【题目】已知圆A:(x+2)2+y2=32,过B(2,0)且与圆A相切的动圆圆心为P.
(1)求点P的轨迹E的方程;
(2)设过点A的直线l1交曲线E于Q、S两点,过点B的直线l2交曲线E于R、T两点,且l1⊥l2,垂足为W(Q、S、R、T为不同的四个点),求四边形QRST的面积的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设动圆半径为r,由于点B在圆A内,所以圆P与圆A内切,计算可得|PA|+|PB|=4![]() |AB|=4,可得点P符合椭圆的定义,可得其轨迹的方程;
|AB|=4,可得点P符合椭圆的定义,可得其轨迹的方程;
(2)若l1或l2的斜率不存在,四边形QRST的面积为8,若两条直线的斜率都存在,设直线l1的斜率为k,则直线l1的方程为y=k(x+2),联立直线与椭圆,设点Q(x1,y1),点S(x2,y2),可得![]() ,
,![]() ,可得|QS|的值,同理可得|RT|,由SQRST
,可得|QS|的值,同理可得|RT|,由SQRST![]() |QS||RT|,利用基本不等式可得其最小值.
|QS||RT|,利用基本不等式可得其最小值.
解:(1)设动圆半径为r,由于点B在圆A内,所以圆P与圆A内切,
∴|PA|=4![]() r,|PB|=r,
r,|PB|=r,
∴|PA|+|PB|=4![]() |AB|=4,
|AB|=4,
∴点P的轨迹是以A,B为焦点的椭圆,其中a=2![]() ,c=2,
,c=2,
∴b2=a2﹣c2=4,
∴点P的轨迹E的方程为:![]() ;
;
(2)若l1或l2的斜率不存在,四边形QRST的面积为8,
若两条直线的斜率都存在,设直线l1的斜率为k,则直线l1的方程为y=k(x+2),
联立方程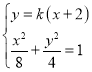 ,得(1+2k2)x2+8k2x+8k2﹣8=0,
,得(1+2k2)x2+8k2x+8k2﹣8=0,
设点Q(x1,y1),点S(x2,y2),
∴![]() ,
,![]() ,
,
∴|QS|![]() 4
4![]() ,
,
同理可得|RT|=4![]()
![]() ,
,
∴SQRST![]() |QS||RT|
|QS||RT|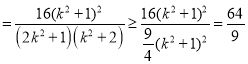 ,当且仅当2k2+1=k2+2,即k=±1时等号成立,
,当且仅当2k2+1=k2+2,即k=±1时等号成立,
综上所述,当k=±1时,四边形QRST的面积取到最小值![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
18 | |||
合计 |
(2)为吸引游客,该超市推出一种优惠方案,购买金额不少于60元可抽奖3次,每次中奖概率为![]() (每次抽奖互不影响,且
(每次抽奖互不影响,且![]() 的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数
的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数![]() (元)的分布列并求其数学期望.
(元)的分布列并求其数学期望.
附:参考公式和数据: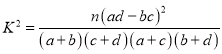 ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
18 | |||
合计 |
(2)为吸引游客,该超市推出一种优惠方案,购买金额不少于60元可抽奖3次,每次中奖概率为![]() (每次抽奖互不影响,且
(每次抽奖互不影响,且![]() 的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数
的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数![]() (元)的分布列并求其数学期望.
(元)的分布列并求其数学期望.
附:参考公式和数据: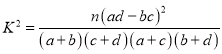 ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |