题目内容
11.向量$|\overrightarrow a|=8,|\overrightarrow b|=12$,则$|\overrightarrow a+\overrightarrow b|$的最大值和最小值的和是24.分析 利用几何运用得出当$\overrightarrow{a}$与$\overrightarrow{b}$同方向时,$|\overrightarrow a+\overrightarrow b|$的最大值,当$\overrightarrow{a}$与$\overrightarrow{b}$反方向时,$|\overrightarrow a+\overrightarrow b|$的最小值即可得出答案.
解答 解:∵向量$|\overrightarrow a|=8,|\overrightarrow b|=12$,

∴当$\overrightarrow{a}$与$\overrightarrow{b}$同方向时,$|\overrightarrow a+\overrightarrow b|$的最大值为12+8=20,
当$\overrightarrow{a}$与$\overrightarrow{b}$反方向时,$|\overrightarrow a+\overrightarrow b|$的最小值为12-8=4,
$|\overrightarrow a+\overrightarrow b|$的最大值和最小值的和是20+4=24
故答案为:24
点评 本题考察了向量的几何运算,分类讨论的思想,属于容易题,关键判断最大值,最小值的情况.

练习册系列答案
相关题目
1.已知函数f(x+1)=3x+1,则f(x)的解析式为( )
| A. | f(x)=3-2x | B. | f(x)=2-3x | C. | f(x)=3x-2 | D. | f(x)=3x |
1.己知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,O为原点,在椭圆上存在一个点P使得△OFP为等边三角形,则椭圆的离心率为( )
| A. | $\sqrt{3}$-1 | B. | 2-$\sqrt{3}$ | C. | $\frac{{\sqrt{5}}}{2}-1$ | D. | $\frac{{\sqrt{5}}}{2}-1$ |
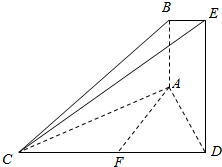 如图所示,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2a,F为CD的中点.
如图所示,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2a,F为CD的中点.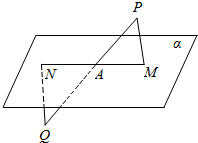 如图,已知直线PM∥QN,PM,QN分别与平面α交于M,N,直线PQ交平面α于A点.求证:M,N,A三点在同一条直线上.
如图,已知直线PM∥QN,PM,QN分别与平面α交于M,N,直线PQ交平面α于A点.求证:M,N,A三点在同一条直线上.