题目内容
【题目】已知函数f（x）=loga 
，（a＞0，且a≠1），
（1）求函数f（x）的定义域．
（2）求使f（x）＞0的x的取值范围．
【答案】
（1）解：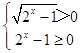 
，解得x＞0，所以函数的定义域为（0，+∞）
（2）解：根据题意，㏒a 
＞0，
当a＞1时， ＞1x＞1；
当0＜a＜1时， ＜1且x＞00＜x＜1
【解析】（1）利用对数的真数大于0，被开方数大于等于0求出定义域．（2）通过对底数a分类讨论；利用函数的单调性将对数函数符号脱去，求出x的范围．
【考点精析】本题主要考查了对数函数的定义域和对数函数的单调性与特殊点的相关知识点，需要掌握对数函数的定义域范围:（0，+∞）；过定点（1，0），即x=1时，y=0;a>1时在（0，+∞）上是增函数;0>a>1时在（0，+∞）上是减函数才能正确解答此题．
练习册系列答案
相关题目
