题目内容
【题目】已知正项数列{an}的前n项和为Sn ， 对任意n∈N* ， 点（an ， Sn）都在函数 
的图象上．
（1）求数列{an}的首项a1和通项公式an；
（2）若数列{bn}满足 
，求数列{bn}的前n项和Tn；
（3）已知数列{cn}满足 
．若对任意n∈N* ， 存在 
，使得c1+c2+…+cn≤f（x）﹣a成立，求实数a的取值范围．
【答案】
（1）解：由题知，当n=1时，a1=S1= 
a12+ a1，所以a1=1（0舍去）．
Sn= an2+ an，所以Sn+1= an+12+ an+1，两式相减得到
（an+1+an）（an+1﹣an﹣1）=0，
因为正项数列{an}，所以an+1﹣an=1，
数列{an}是以1为首项，1为公差的等差数列，所以an=n．
（2）解：由（1）知an=n，{bn}满足 
=n+log2（2n﹣1），
所以bn=（2n﹣1）2n，
因此前n项和Tn=121+322+523+…+（2n﹣1）2n，①
2Tn=122+323+524+…+（2n﹣1）2n+1，②
由①﹣②得到﹣Tn=2+2（22+23+…+2n）﹣（2n﹣1）2n+1
=2+2 
﹣（2n﹣1）2n+1=﹣6+（3﹣2n）2n+1，
所以Tn=6+（2n﹣3）2n+1．
（3）解：由（2）知Tn=6+（2n﹣3）2n+1，
= 
﹣ 
= ﹣（ 
﹣ 
）．
令Mn为数列{cn}的前n项和，
易得Mn= 
﹣（1﹣ + ﹣ 
+…+ ﹣ 
）= ﹣ ．
因为c1=0，c2＞0，c3＞0，c4＞0，当n≥5时，cn= [ 
﹣1]，
而 ﹣ 
= 
＞0，得到
≤ 
＜1，所以当n≥5时，cn＜0，所以Mn≤M4= 
﹣ 
= 
﹣ 
．
又x∈[﹣ ， ]，f（x）﹣a= x2+ x﹣a递增，可得其最大值为 
﹣a．
因为对任意的n∈N*，存在x0∈[﹣ ， ]，使得Mn≤f（x）﹣a成立．
所以 ﹣ ≤ ﹣a，
解得a≤ 
．
【解析】（1）运用数列的递推式，令n=1，求出首项；再将n换为n+1，两式相减，化简即可得到所求通项公式；（2）运用对数的运算性质可得bn=（2n﹣1）2n ， 再由数列的求和方法：错位相减法，结合等比数列的求和公式，计算即可得到所求和；（3）求得 
= ﹣ = ﹣（ ﹣ ）．运用分组求和和裂项相消求和，可得Mn= ﹣ ．讨论{Mn}的单调性，可得最大值M4 ， 求得f（x）﹣a的最大值，由题意可得a的不等式，解不等式即可得到所求范围．
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系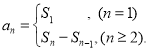
，以及对数列的通项公式的理解，了解如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
