题目内容
【题目】已知函数f（x）=loga 
，（a＞0且a≠1）．
（1）判断f（x）的奇偶性，并加以证明；
（2）是否存在实数m使得f（x+2）+f（m﹣x）为常数？若存在，求出m的值；若不存在，说明理由．
【答案】
（1）
解：f（x）=loga 
为奇函数，下面证明：
解 ＞0可得定义域为{x|x＜﹣5或x＞5}，关于原点对称，
f（﹣x）=loga
=﹣loga =﹣f（x），
∴函数f（x）为奇函数
（2）
解：假设存在这样的m，则f（x+2）+f（m﹣x）
=loga
=loga 
，
∴ 为常数，设为k，
则（k﹣1）x2+（m﹣2）（1﹣k）x﹣3（m﹣5）﹣7k（m+5）=0对定义域内的x恒成立
∴ 
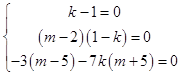，解得 
∴存在这样的m=﹣2
【解析】（1）f（x）=loga 为奇函数，求函数的定义域并利用奇函数的定义证明即可；（2）假设存在这样的m，则f（x+2）+f（m﹣x）=loga ，即 为常数，设为k，整理由多项式系数相等可得m和k的方程组，解方程组可得．
练习册系列答案
相关题目
