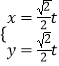题目内容
【题目】设D为不等式组  ,表示的平面区域,点B(a,b)为第一象限内一点,若对于区域D内的任一点A(x,y)都有
,表示的平面区域,点B(a,b)为第一象限内一点,若对于区域D内的任一点A(x,y)都有 ![]() 成立,则a+b的最大值等于( )
成立,则a+b的最大值等于( )
A.0
B.1
C.2
D.3
【答案】C
【解析】解:∵点B(a,b)为第一象限内一点,∴a>0,b>0,
又区域D内的任一点A(x,y),
∴z= ![]() ,
,
由约束条件 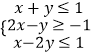 作出可行域如图:
作出可行域如图:
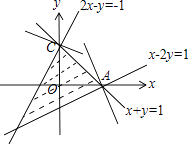
化z=ax+by为y= ![]() ,
,
由图可知,当 ![]() ,即a≥b时,
,即a≥b时,
直线y= ![]() 过A(1,0)时,直线在y轴上的截距最大,z有最大值为a,则a≤1;
过A(1,0)时,直线在y轴上的截距最大,z有最大值为a,则a≤1;
当 ![]() ,即a<b时,直线y=
,即a<b时,直线y= ![]() 过C(0,1)时,
过C(0,1)时,
直线在y轴上的截距最大,z有最大值为b,则b≤1.
∴点B(a,b)满足  或
或 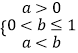 .
.
作出可行域如图:
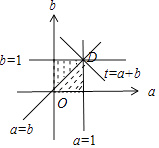
令t=a+b,化为b=﹣a+t,由图可知,当直线b=﹣a+t过D(1,1)时,
直线在b轴上的截距最大,t有最大值为1+1=2.
故选:C.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目