Question

【题目】北宋数学家沈括的主要数学成就之一为隙积术，所谓隙积，即“积之有隙”者，如累棋、层坛之类，这种长方台形状的物体垛积．设隙积共n层，上底由长为a个物体，宽为b个物体组成，以下各层的长、宽依次各增加一个物体，最下层成为长为c个物体，宽为d个物体组成，沈括给出求隙积中物体总数的公式为S= ．已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示，则该垛积中所有小球的个数为 ．

Answer 1

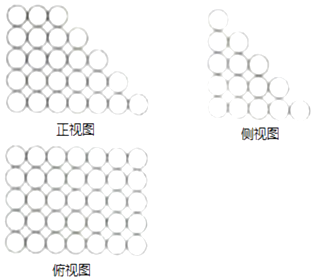
【答案】85
【解析】解：由题意，a=3，b=1，c=7，d=5，n=5，

∴S= [（2b+d）a+（b+2d）c]+ （c﹣a）= [3×（2+5）+7×（1+10）]+ （7﹣3）=85，

所以答案是：85．

【考点精析】解答此题的关键在于理解归纳推理的相关知识，掌握根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理．