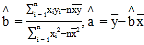��Ŀ����
����Ŀ��������Ժ����ͬ�⣬֣�ݳɹ���Χ�������ij��У�ijУѧ������ԡ�֣�ݵķ�չ��������20��ѧ�������ʾ������֣�����100�֣����õ���ͼ1��ʾ��Ҷͼ�� 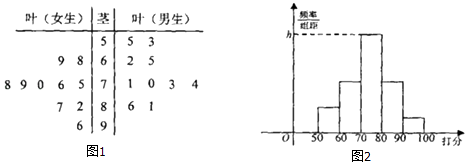
���ֱ��������Ů����ֵ�ƽ���֣�������ѧ����������Ů����ֵ����ݷֲ������
������ͼ2���մ������[0��60����[60��70����[70��80����[80��90����[90��100]���Ƶ�ֱ��ͼ�У�����߾��εĸߣ�
���Ӵ����70�����£�����70�֣���ͬѧ�г�ȡ3�ˣ�����Ů�������еĸ��ʣ�
���𰸡��⣺����Ů����ֵ�ƽ����Ϊ��
![]() =
= ![]() ��68+69+75+76+70+79+78+82+87+96��=78��
��68+69+75+76+70+79+78+82+87+96��=78��
������ֵ�ƽ����Ϊ��
![]() =
= ![]() ��55+53+62+65+71+70+73+74+86+81��=69��
��55+53+62+65+71+70+73+74+86+81��=69��
�Ӿ�Ҷͼ������Ů�������Լ��У����������Է�ɢ��
����20��ѧ���У��������[0��60����[60��70����[70��80����[80��90����[90��100]�е�ѧ�����ֱ�Ϊ��
2�ˣ�4�ˣ�9�ˣ�4�ˣ�1�ˣ�
�������[70��80����������࣬��9�ˣ�����Ƶ��Ϊ�� ![]() =0.45��
=0.45��
����߾��εĸ�h= ![]() =0.045��
=0.045��
�������70�����£�����70�֣���ͬѧ��6�ˣ���������4�ˣ�Ů��2�ˣ�
���г�ȡ3�ˣ������¼�����n= ![]() =20��
=20��
��Ů�������еĶ����¼��dz��е�3��ͬѧ����������
����Ů�������еĸ���p=1�� ![]() =1��
=1�� ![]() =
= ![]() ��
��
���������������þ�Ҷͼ�����Ů����ֵ�ƽ���ֺ�������ֵ�ƽ���֣��Ӿ�Ҷͼ������Ů�������Լ��У����������Է�ɢ��
����20��ѧ���У��������[0��60����[60��70����[70��80����[80��90����[90��100]�е�ѧ�����ֱ�Ϊ��2�ˣ�4�ˣ�9�ˣ�4�ˣ�1�ˣ��������[70��80����������࣬��9�ˣ�����Ƶ��Ϊ0.45���ɴ��������߾��εĸߣ�
�������70�����£�����70�֣���ͬѧ��6�ˣ���������4�ˣ�Ů��2�ˣ���Ů�������еĶ����¼��dz��е�3��ͬѧ�����������ɴ����ö����¼����ʼ��㹫ʽ�������Ů�������еĸ��ʣ�
�����㾫����ͨ���������Ƶ�ʷֲ�ֱ��ͼ�;�Ҷͼ������Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ����Ҷͼ�ֳơ�֦Ҷͼ��������˼·�ǽ������е�����λ�����бȽϣ������Ĵ�С���������仯�����λ��Ϊһ�����ɣ����������仯���λ������Ϊ��֦��Ҷ�����������ɵĺ��棬�����Ϳ�������ؿ���ÿ�����ɺ���ļ�������ÿ���������Ƕ��ټ����Խ����⣮