题目内容
函数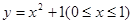 图象上点P处的切线与直线
图象上点P处的切线与直线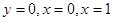 围成的梯形面积等于S,则S的最大值等于 ,此时点P的坐标是 .
围成的梯形面积等于S,则S的最大值等于 ,此时点P的坐标是 .
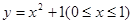 图象上点P处的切线与直线
图象上点P处的切线与直线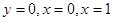 围成的梯形面积等于S,则S的最大值等于 ,此时点P的坐标是 .
围成的梯形面积等于S,则S的最大值等于 ,此时点P的坐标是 .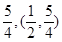
设P点坐标为(a,a2+1)则得到在P处的切线方程,利用定积分的方法求出梯形的面积,求出面积的最大值即可得到P的坐标.
解:设P(a,a2+1)则过P的切线方程为:y=2ax-a2+1
则S=∫01(2ax-a2-1)dx=(3x-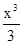 -x2)|01=-a2+a+1为二次函数,
-x2)|01=-a2+a+1为二次函数,
当a= 时,S有最大值,Smax=
时,S有最大值,Smax=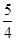 .且此时P的坐标为(
.且此时P的坐标为( ,
,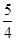 ).
).
故答案为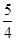 ,(
,( ,
,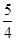 )
)
解:设P(a,a2+1)则过P的切线方程为:y=2ax-a2+1
则S=∫01(2ax-a2-1)dx=(3x-
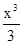 -x2)|01=-a2+a+1为二次函数,
-x2)|01=-a2+a+1为二次函数,当a=
 时,S有最大值,Smax=
时,S有最大值,Smax=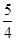 .且此时P的坐标为(
.且此时P的坐标为( ,
,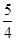 ).
).故答案为
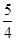 ,(
,( ,
,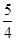 )
)
练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目
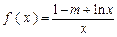 ,
,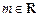 .
.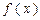 的极值;
的极值;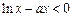 在
在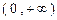 上恒成立,求
上恒成立,求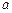 的取值范围.
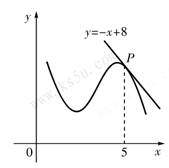
的取值范围.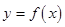 的图象在点P处的切线方程是
的图象在点P处的切线方程是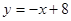 ,则
,则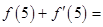 ( )
( )
 B.
B. C.2 D.0
C.2 D.0 的定义域为R+,若对于给定的正数K,定义函数
的定义域为R+,若对于给定的正数K,定义函数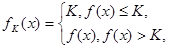 ,则当函数
,则当函数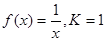 时,定积分
时,定积分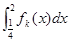 的值为
的值为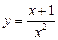 (
(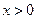 )上横坐标为1的点的切线方程为
)上横坐标为1的点的切线方程为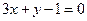
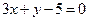
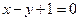
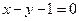
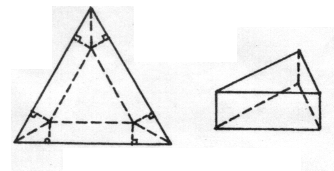
 .工人师傅计划用它加工成一个无盖直三棱柱型水箱,设计方案为:将图中的阴影部分切去,再把它沿虚线折起,请计算水箱的高为多少时,水箱的容积最大?最大容积是多少?
.工人师傅计划用它加工成一个无盖直三棱柱型水箱,设计方案为:将图中的阴影部分切去,再把它沿虚线折起,请计算水箱的高为多少时,水箱的容积最大?最大容积是多少?
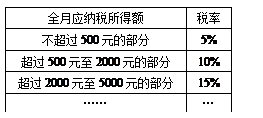
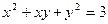 ,求
,求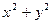 的范围.
的范围.