题目内容
【题目】已知椭圆C的方程为 
+ 
=1（a＞b＞0），双曲线 ﹣ =1的一条渐近线与x轴所成的夹角为30°，且双曲线的焦距为4 
．
（1）求椭圆C的方程；
（2）设F1 ， F2分别为椭圆C的左，右焦点，过F2作直线l（与x轴不重合）交于椭圆于A，B两点，线段AB的中点为E，记直线F1E的斜率为k，求k的取值范围．
【答案】
（1）解：由一条渐近线与x轴所成的夹角为30°，则 
=tan30°= 
，即a2=3b2，
由2c=4 
．c=2 ，则a2+b2=8，
解得：a2=8，b2=2，
∴椭圆的标准方程： 
（2）解：由（1）可知：F2（2，0），直线AB的方程：x=ty+2，A（x1，y1），B（x2，y2），
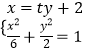，整理得：（t2+3）y2+4ty﹣2=0，
y1+y2=﹣ 
，x1+x2= 
，
则E（ 
，﹣ 
），
由F1（﹣2，0），则直线F1E的斜率k=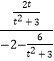 
=﹣ 
，
①当t=0时，k=0，
②当t≠0时，丨k丨= 
= 
≤ 
，
即丨k丨∈（0， 
]，
∴k的取值范围[﹣ ， ]
【解析】（1）由双曲线的渐近线方程及斜率公式，即可求得a2=3b2，c=2 ，即a2+b2=8，即可求得a和b的值，求得椭圆方程；（2）设直线AB的方程，代入椭圆方程，利用韦达定理求得斜率丨k丨用t表示，利用基本不等式即可求得k的取值范围．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
