题目内容
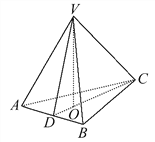
【题目】如图四边形ABCD为边长为2的菱形,G为AC与BD交点,平面BED⊥平面ABCD,BE=2,AE=2 ![]() .
. 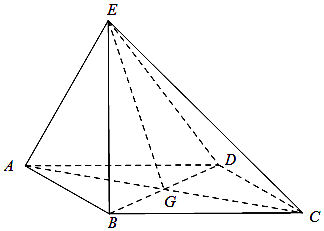
(Ⅰ)证明:BE⊥平面ABCD;
(Ⅱ)若∠ABC=120°,求直线EG与平面EDC所成角的正弦值.
【答案】解:(Ⅰ)证明:∵四边形ABCD为菱形,∴AC⊥DB
又因为平面BED⊥平面ABCD,平面BED∩平面ABCD=DB,AC平面ABCD.
∴AC⊥平面BED,即AC⊥BE.
又BE=2,AE=2 ![]() ,AB=2,∴AE2=AB2+BE2,
,AB=2,∴AE2=AB2+BE2,
∴BE⊥AB,且AB∩BD=B,∴BE⊥平面ABCD.
(Ⅱ)取AD中点H,连接BH.
∵四边形ABCD为边长为2的菱形,∠ABC=120°,∴BH⊥AD,且BH= ![]() .
.
由(Ⅰ)得BE⊥平面ABCD,故以B为原点,建立空间直角坐标系(如图)
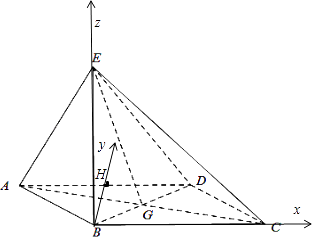
则E(0,0,2),D(1, ![]() ,0),G(
,0),G( ![]() ,
, ![]() ,0),C(2,0,0)
,0),C(2,0,0)
设面EDC的法向量为 ![]()
![]() ,
, ![]() ,
, 
由 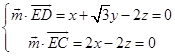 ,可取
,可取 ![]()
cos ![]() =
= 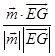 =﹣
=﹣ ![]()
直线EG与平面EDC所成角的正弦值为 ![]()
【解析】(Ⅰ)由AC⊥DB,平面BED⊥平面ABCD,得AC⊥平面BED,即AC⊥BE.
又 AE2=AB2+BE2,得BE⊥AB,即可得BE⊥平面ABCD.(Ⅱ)由(Ⅰ)得BE⊥平面ABCD,故以B为原点,建立空间直角坐标系,
则E(0,0,2),D(1, ![]() ,0),G(
,0),G( ![]() ,
, ![]() ,0),C(2,0,0),利用向量法求解.
,0),C(2,0,0),利用向量法求解.
【考点精析】根据题目的已知条件,利用直线与平面垂直的判定和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则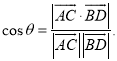 .
.

【题目】“菊花”型烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点时爆裂.通过研究,发现该型烟花爆裂时距地面的高度![]() (单位:米)与时间
(单位:米)与时间![]() (单位:秒)存在函数关系,并得到相关数据如表:
(单位:秒)存在函数关系,并得到相关数据如表:
时间 | 1 |
|
|
高度 |
|
|
|
(1)根据表中数据,从下列函数中选取一个函数描述该型烟花爆裂时距地面的高度![]() 与时间
与时间![]() 的变化关系:
的变化关系: ![]() ,
, ![]() ,
, ![]() ,确定此函数解析式并简单说明理由;
,确定此函数解析式并简单说明理由;
(2)利用你选取的函数,判断烟花爆裂的最佳时刻,并求此时烟花距地面的高度.