题目内容
【题目】水培植物需要一种植物专用营养液,已知每投放![]() (
(![]() 且
且![]() )个单位的营养液,它在水中释放的浓度
)个单位的营养液,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (天)变化的函数关系式近似为
(天)变化的函数关系式近似为![]() ,其中
,其中 ,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
(1)若只投放一次2个单位的营养液,则有效时间最多可能达到几天?
(2)若先投放2个单位的营养液,3天后再投放![]() 个单位的营养液,要使接下来的2天中,营养液能够持续有效,试求
个单位的营养液,要使接下来的2天中,营养液能够持续有效,试求![]() 的最小值.
的最小值.
【答案】(1) 3天;(2) ![]() .
.
【解析】试题分析:(1)由题意可知营养液有效则需满足![]() ,由此得
,由此得 或
或![]() ,解不等式可得
,解不等式可得![]() ,故最多可达3天;(2)设
,故最多可达3天;(2)设![]() ,
, ![]() 分别为第一、二次投放营养液的浓度,
分别为第一、二次投放营养液的浓度, ![]() 为水中的营养液的浓度,由题意得
为水中的营养液的浓度,由题意得![]() 在
在![]() 上恒成立,可得
上恒成立,可得![]() 在
在![]() 上恒成立,求得
上恒成立,求得![]() 在
在![]() 上的最大值即可得到
上的最大值即可得到![]() 的最小值。
的最小值。
试题解析:
(1)营养液有效则需满足![]() ,
,
则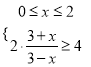 或
或![]() ,
,
即为![]() 或
或![]() ,
,
解得![]() ,
,
所以营养液有效时间最多可达3天;
(2)解法一:设第二次投放营养液的持续时间为![]() 天,
天,
则此时第一次投放营养液的持续时间为![]() 天,且
天,且![]() ;
;
设![]() 为第一次投放营养液的浓度,
为第一次投放营养液的浓度, ![]() 为第二次投放营养液的浓度,
为第二次投放营养液的浓度, ![]() 为水中的营养液的浓度;
为水中的营养液的浓度;
∴![]() ,
,
![]() ,
,
由题意得![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,则
,则![]() ,
,
又![]() ,
,
当且仅当![]() ,即
,即![]() 时等号成立;
时等号成立;
因为![]()
所以![]() 的最小值为
的最小值为![]() .
.
答:要使接下来的2天中,营养液能够持续有效, ![]() 的最小值为
的最小值为![]() .
.
解法二:设两次投放营养液后的持续时间为![]() 天,
天,
则第一次投放营养液的持续时间为![]() 天,
天,
第二次投放营养液的持续时间为![]() 天,且
天,且![]() ,
,
设![]() 为第一次投放营养液的浓度,
为第一次投放营养液的浓度, ![]() 为第二次投放营养液的浓度,
为第二次投放营养液的浓度, ![]() 为水中的营养液的浓度;
为水中的营养液的浓度;
∴![]() ,
,
![]()
由题意得![]() 在
在![]() 上恒成立
上恒成立
∴![]() 在
在![]() 上恒成立
上恒成立
则![]()
又![]() ,
,
当且仅当![]() 即
即![]() 时等号成立;
时等号成立;
因![]() ,
,
所以![]() 的最小值为
的最小值为![]() .
.
答:要使接下来的2天中,营养液能够持续有效, ![]() 的最小值为
的最小值为![]() .
.

【题目】学生会为了调查学生对2018年俄罗斯世界杯的关注是否与性别有关,抽样调查100人,得到如下数据:
不关注 | 关注 | 总计 | |
男生 | 30 | 15 | 45 |
女生 | 45 | 10 | 55 |
总计 | 75 | 25 | 100 |
根据表中数据,通过计算统计量K2= ![]() ,并参考一下临界数据:
,并参考一下临界数据:
P(K2>k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
若由此认为“学生对2018年俄罗斯年世界杯的关注与性别有关”,则此结论出错的概率不超过( )
A.0.10
B.0.05
C.0.025
D.0.01
【题目】“菊花”型烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点时爆裂.通过研究,发现该型烟花爆裂时距地面的高度![]() (单位:米)与时间
(单位:米)与时间![]() (单位:秒)存在函数关系,并得到相关数据如表:
(单位:秒)存在函数关系,并得到相关数据如表:
时间 | 1 |
|
|
高度 |
|
|
|
(1)根据表中数据,从下列函数中选取一个函数描述该型烟花爆裂时距地面的高度![]() 与时间
与时间![]() 的变化关系:
的变化关系: ![]() ,
, ![]() ,
, ![]() ,确定此函数解析式并简单说明理由;
,确定此函数解析式并简单说明理由;
(2)利用你选取的函数,判断烟花爆裂的最佳时刻,并求此时烟花距地面的高度.