题目内容
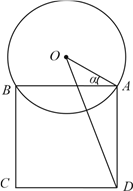
【题目】某校一个校园景观的主题为“托起明天的太阳”,其主体是一个半径为5米的球体,需设计一个透明的支撑物将其托起,该支撑物为等边圆柱形的侧面,厚度忽略不计.轴截面如图所示,设![]() .(注:底面直径和高相等的圆柱叫做等边圆柱.)
.(注:底面直径和高相等的圆柱叫做等边圆柱.)
(1)用![]() 表示圆柱的高;
表示圆柱的高;
(2)实践表明,当球心![]() 和圆柱底面圆周上的点
和圆柱底面圆周上的点![]() 的距离达到最大时,景观的观赏效
的距离达到最大时,景观的观赏效
果最佳,求此时![]() 的值.
的值.
【答案】(1)![]() (2)当
(2)当![]() 时,观赏效果最佳.
时,观赏效果最佳.
【解析】试题分析:
(1)做出辅助线,结合图形的特点可得![]() ;
;
(2)结合余弦定理可得![]() 结合三角函数的性质有当
结合三角函数的性质有当![]() 时,观赏效果最佳.
时,观赏效果最佳.
试题解析:
(1)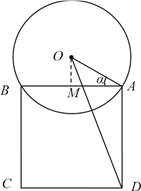 作
作![]() 于点
于点![]() ,则在直角三角形
,则在直角三角形![]() 中,
中,
因为![]() ,
,
所以![]() ,
,
因为四边形![]() 是等边圆柱的轴截面,
是等边圆柱的轴截面,
所以四边形![]() 为正方形,
为正方形,
所以![]() .
.
(2)由余弦定理得:
![]() ,……8分
,……8分
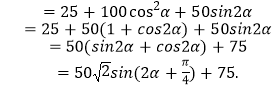
因为![]() ,所以
,所以![]() ,
,
所以当![]() ,即
,即![]() 时,
时,![]() 取得最大值
取得最大值![]()
![]() ,
,
所以当![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.
答:当![]() 时,观赏效果最佳.
时,观赏效果最佳.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
【题目】学生会为了调查学生对2018年俄罗斯世界杯的关注是否与性别有关,抽样调查100人,得到如下数据:
不关注 | 关注 | 总计 | |
男生 | 30 | 15 | 45 |
女生 | 45 | 10 | 55 |
总计 | 75 | 25 | 100 |
根据表中数据,通过计算统计量K2= ![]() ,并参考一下临界数据:
,并参考一下临界数据:
P(K2>k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
若由此认为“学生对2018年俄罗斯年世界杯的关注与性别有关”,则此结论出错的概率不超过( )
A.0.10
B.0.05
C.0.025
D.0.01