题目内容
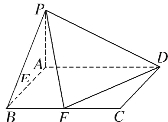
【题目】如图，已知四棱锥
的底面为矩形，平面
平面
， 
， 
，则四棱锥
的外接球的表面积为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
取AD的中点E，连接PE，△PAD中，PA=PD=1， 
，
∴PA⊥PD，∴PE=
，设ABCD的中心为O′，球心为O，则O′B=
BD=
，
设O到平面ABCD的距离为d，则R2=d2+（
）2=
+（
﹣d）2，
∴d=0，R=
，∴四棱锥P﹣ABCD的外接球的表面积为4πR2=3π．故选：A．
点睛:空间几何体与球接、切问题的求解方法
(1)求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．
(2)若球面上四点
构成的三条线段
两两互相垂直，且
，一般把有关元素“补形”成为一个球内接长方体，利用
求解．
练习册系列答案
相关题目
【题目】学生会为了调查学生对2018年俄罗斯世界杯的关注是否与性别有关，抽样调查100人，得到如下数据：
不关注 | 关注 | 总计 | |
男生 | 30 | 15 | 45 |
女生 | 45 | 10 | 55 |
总计 | 75 | 25 | 100 |
根据表中数据，通过计算统计量K2= 
，并参考一下临界数据：
P（K2＞k0） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
若由此认为“学生对2018年俄罗斯年世界杯的关注与性别有关”，则此结论出错的概率不超过（ ）
A.0.10
B.0.05
C.0.025
D.0.01
